Geoid

Jordens tyngdekraftsfelt: lodd gjennom overflatepunkt P, potensialutjevningsflater V _i og geoiden (potensial V = V _o ) som en fortsettelse av gjennomsnittlig havnivå.

Geoiden er en viktig referanseoverflate i jordens gravitasjonsfelt . Den brukes til å definere høyder så vel som å måle og beskrive jordens figur . ^[1] For en god tilnærming er geoiden representert ved gjennomsnittlig havnivå i verdenshavene og er dermed direkte synlig i sin form utenfor landmassene .

Overflatene til geoidet er definert som områdene med like gravitasjonspotensial . Dette gjør den geoide overflaten på havnivå til den mest informative, men alle andre overflater er likeverdige. Den naturlige loddlinjen og geoidflatene er derfor vinkelrett på hverandre på hvert punkt. Derfor kan geoiden bestemmes ved å måle akselerasjonen på grunn av tyngdekraften . Alle to punkter på geoiden har samme gravitasjonspotensial og derfor samme dynamiske høyde .

I motsetning til gravitasjonspotensialet er gravitasjonsakselerasjonen g ikke konstant på geoiden. På grunn av den økende sentrifugale akselerasjonen fra polen til ekvator synker den fra 9,83 til 9,78 m / s². ^[2] I tillegg varierer det lokalt på grunn av den inhomogene massefordelingen av jorden.

Geoiden er en fysisk modell av jordfiguren, som ble beskrevet av Carl Friedrich Gauß i 1828 - i motsetning til den geometriske modellen av jordelipsoiden . Navnet geoid går tilbake til Johann Benedict Listing , som beskrev det i 1871 som et område med like gravitasjonspotensial: Geoid er det potensialområdet for jordens gravitasjonsfelt på gjennomsnittlig havnivå, dvs. alle punkter som har samme geopotensial, består av gravitasjonspotensialet og sentrifugalpotensialet på det aktuelle stedet.

Jordfigur og geoid

Havnivået er - bortsett fra strømmer og tidevann - en såkalt nivåoverflate som gravitasjonspotensialet er konstant på fordi det er overalt vinkelrett på lodden. Det er sant at det er uendelig mange slike potensialflater som løper rundt midten av jorden som løkskinn. Det særegne ved havnivået er imidlertid at det kan observeres over hele verden gjennom nivåobservasjon og er derfor egnet som en global referanseoverflate for høydemålinger og tyngdekraftmålinger. For dette formålet har noen europeiske land satt opp og målt nivåer på forskjellige kyststeder for rundt 200 år siden, for eksempel Amsterdam -nivået eller nivåstasjonene i Trieste , Genova , Marseille og St. Petersburg . Forbindelsen deres over land, muliggjort av høydenettverk, ville ha vært egnet for å bestemme den kontinentale geoiden, men dette ble ikke gjort før de europeiske nettverkene på 1900 -tallet av politiske årsaker.

Den regionale bestemmelsen av geoidoverflaten ble først utført ved astrogeodetisk bestemmelse av den vinkelrette retningen til individuelle undersøkelsespunkter og fra 1930-årene gjennom profil- eller rutenettlignende skala tyngdekraftmålinger med gravimetre . Astrogeoider og gravimetrisk geoidbestemmelse har blitt merkbart forbedret av landmålingskontorene siden rundt 1970 gjennom sterk komprimering av de vertikale avviks- eller tyngdekraftnettverkene , mens global nøyaktighet har blitt økt gjennom år med satellitthøyde over havet.

De automatiserte metodene for satellittgeodesi dominerer bestemmelsen av jordens tyngdekraftsfelt. De viser geoiden som en uregelmessig overflate med mange støt og bulker, men de utgjør bare omtrent 0,001 prosent av jordens radius . Disse bølgelignende geoidformene skyldes tyngdekraftanomalier i fjellene og ujevn massefordeling i jordens indre.

På grunn av sin uregelmessige form er geoiden svært vanskelig å beskrive matematisk, mens praktisk landmåling , kartografi og GPS -posisjonering krever en mer enkelt definert figur av jorden. Slike referanseflater for beregninger og kartbilder er for det meste ellipsoider av revolusjon som tilnærmer geoidet til en nøyaktighet på omtrent 50 m. Imidlertid kan disse strengt matematiske områdene ikke bestemmes direkte ved å måle fysiske mengder .

For praktisk bruk må avviket mellom den fysiske jordfiguren (geoid) og den matematiske motparten som er egnet for beregninger (rotasjonsellipsoid) bestemmes ved systematiske målinger . Geoidens avvik fra en referanse -ellipsoid (f.eks. WGS84 , GRS 80 , Internationales Ellipsoid 1924 ) omtales som geoidbølging eller geoidhøyde og kan være opptil 100 m og variere med omtrent ± 30 m over 1000 km:

Geoidbølging

N=h-H

{\ displaystyle N = hH}

N = h-H

, med ellipsoidal (geometrisk) høyde

H

{\ displaystyle h}

H

og ortometrisk (fysisk) høyde

H

{\ displaystyle H}

H

Geoid -tilnærminger med sfæriske funksjoner

Pæreform som en tilnærming til jordfiguren sammenlignet med det elliptiske tverrsnittet (svart linje).

Illustrasjon av variasjonen i tyngdekraften langs ekvator, basert på en sirkulær referanseflate (svart).

I den nulte tilnærmelse , forsømmes potensialet av sentrifugalkraften U _z, er den geoide en ekvipotensialflate i gravitasjonsfeltet til et massepunkt: u (r) = G M / r + U _z (G: gravitasjonskonstanten , M: jordens masse, r : avstand fra midten av jorden). Denne forenklingen gir nyttige resultater for mange beregninger innen himmelsk mekanikk og romfart . Geoiden er en kule med en parameter R ≈ 6373 km for radius.

Avvik fra den sfæriske formen kan beskrives av Legendre polynom P _n (cos ( θ )) ( θ : breddegradvinkel, R : gjennomsnittlig jordradius, J _n : ekspansjonskoeffisienter):

U(r,\theta )={\frac {GM}{r}}\sum _{n=0,1,\dots }\left(\left({\frac {R}{r}}\right)^{n}J_{n}\cdot P_{n}\left(\cos(\theta )\right)\right)+U_{\mathrm {z} }

{\ displaystyle U (r, \ theta) = {\ frac {GM} {r}} \ sum _ {n = 0.1, \ dots} \ left (\ left ({\ frac {R} {r}} \ right ) ^ {n} J_ {n} \ cdot P_ {n} \ venstre (\ cos (\ theta) \ høyre) \ høyre) + U _ {\ mathrm {z}}}

U (r, \ theta) = \ frac {GM} {r} \ sum_ {n = 0, 1, \ dots} \ venstre (\ venstre (\ frac {R} {r} \ høyre) ^ n J_n \ cdot P_n \ venstre (\ cos (\ theta) \ høyre) \ høyre) + U_ \ mathrm {z}

med koeffisientene:

J ₀ = 1; Ball tilnærming

J ₁ = 0; ingen dipolmoment, nordlige og sørlige halvkule like tunge

_J2 = 1082,6 x 10 ^-6; Omtrentlig figur av jorden som en revolusjonens ellipsoid med ekvatoriale halvakser av samme størrelse a = b ≈ 6378 km og c ≈ 6357 km som polaraksen. J ₂ tar hensyn til den såkalte andreordens massefunksjonen , som kommer fra utflating av jorden

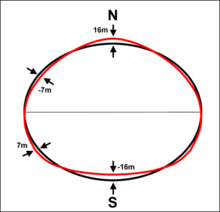
J ₃ = 2,51 x 10 ^-6; Sett en pære-lignende struktur på ellipsoiden (se tegning)

J ₄ = 1,60 · 10 ⁻⁶

Massefunksjonene J ₃ og J ₄ forårsaker geometriske avvik fra gjennomsnittlig jordelipsoid som er mindre enn 20 m. Den høye høyden på tegningen til høyre illustrerer hvorfor jorden noen ganger beskrives som "pæreformet".

En forbedret tilnærming introduserer ytterligere sfæriske funksjonskoeffisienter som tar hensyn til noen av geoidens avhengigheter av lengdegrad . Den skjematiske tegningen til høyre gjør det klart at det er avvik i tyngdekraften i lengdegraden, som tilsvarer en høydeforskjell på 170 m. De er grunnen til at det bare er to stabile og to ustabile bane posisjoner for geostasjonære satellitter .

Geoid bestemmelse

Målte avvik fra jordens gravitasjonsfelt fra revolusjonens ellipsoid.

Tredimensjonal modell av "Potsdam Potato" (2017) med en 15 000 ganger forsterket representasjon av høydeavviket, tysk forskningssenter for geofag

Den mest presise bestemmelsen av hele geoiden så langt ble utført av GRACE -prosjektet. Den består av to satellitter som kretser rundt jorden i en avstand på omtrent 200 km i samme høyde. Avstanden mellom de to satellittene måles konstant med høy grad av nøyaktighet. Formen på geoiden kan deretter utledes av endringen i denne avstanden.

Geoidbestemmelsen kan også utføres med metoder for astrogeodesi eller gravimetrisk; begge gir de detaljerte formene til geoiden mer presist enn satellittene, men er mer komplekse. Bestemmelsen av astrogeoid (måling av det vertikale avviket ) ble testet for 100 år siden og er den mest nøyaktige metoden, men krever et undersøkelsesnettverk og klare netter for stjerneobservasjon. Det ideelle astrogeodesi -instrumentet for dette er zenitkameraet : med sin hjelp kan den vinkelrette retningen på et målepunkt bestemmes med høy presisjon og delvis automatisk ved hjelp av CCD -bilder av zenithal -stjernefeltet. Disse loddlinjene forholder seg til gravitasjonsfeltet og dermed til geoidet. For å bestemme hellingen til geoiden med hensyn til referanse -ellipsoiden fra vertikale avvik, er det nødvendig å kjenne ellipsoide koordinatene til målepunktet. Disse kan bestemmes ut fra den nasjonale undersøkelsen eller med GNSS -navigasjonssatellitter.

I gravimetri bestemmes geoiden ved å måle akselerasjonen på grunn av tyngdekraften i form av et rutenett. Imidlertid er metoden for kompleks for global geoidbestemmelse gjennom en tilstrekkelig tett fordeling av målepunktene. En digital terrengmodell er fordelaktig for geoidinterpolasjon mellom målepunktene i fjellet - akkurat som med astrogeoiden.

I juni 2011 publiserte det tyske forskningssenteret for geofag (GFZ) i Potsdam den tunge modellen " EIGEN-6C ", som har blitt kjent som Potsdam-poteten . ^[3] ^[4] ^[5] Denne globale modellen ble laget av de kombinerte dataene fra forskjellige satellittmålinger fra LAGEOS , GRACE , GOCE og andre målemetoder og har en romlig oppløsning på ca. 12 km.

Årsaker til geoidbølger

Tette anomalier i jordens mantel på grunn av mantelkonveksjon og tilhørende variasjoner i topografi er årsaken til flertallet av de observerte geoidbølgene.

Årsakene til de lange, bølgete geoidfluktuasjonene (geoidbølger) ligger i store tetthetsvariasjoner i jordkappen og, i mindre grad, i jordskorpen . En unormalt høyere bergtetthet skaper en ekstra gravitasjonsakselerasjon og buler dermed geoidet, lavere tettheter fører til "bulker" i geoiden. Men selve topografien representerer også en sideveis variabel massevariasjon (→ heving (geologi) ) og fører til bølger. Årsaken til tetthetsvariasjoner i jordens mantel ligger i mantelkonveksjon: varme mantelområder er mindre tette og stiger (→ fjær (geologi) ); kalde, tette områder synker.

Man ville nå forvente "bulker" i geoiden fra stigende konveksjonsstrømmer, og "støt" fra synkende konveksjonsstrømmer (f.eks. Over subduksjonssoner ), som i det store og hele er enig med observasjonene for Vest -Stillehavet . Ting blir imidlertid mer komplisert av det faktum at stigende konveksjonsstrømmer kan heve overflaten på jorden selv (f.eks. Island , Hawaii ). Topografien som er opprettet på denne måten kalles " dynamisk topografi". Dette svekker den faktiske negative geoidbølgen og noen ganger reverserer den til det positive området (som Island ser ut til å være et eksempel på). Videre avhenger effekten av den dynamiske topografien også av viskositeten til jordkappen og er vanskelig å kvantifisere .

Spesielt funn fra seismologi brukes til å estimere tettheter i mantelen og for å beregne geoid og dynamisk topografi. Konklusjoner om jakkens viskositet kan trekkes fra sammenligningen med den observerte geoiden.

Moderne geoidløsninger

Fram til rundt 1970 kunne eksakte geoidbestemmelser nesten utelukkende utføres på fastlandet , og derfor kalles de noen ganger regional geoid :

som en astrogeoid basert på vertikale avvik , hentet fra en kombinasjon av astronomiske og geodetiske metoder,
på den annen side som en gravimetrisk geoid ved hjelp av rutenettformede tyngdekraftmålinger , slik de er nødvendige for geodetisk presisjonsutjevning og i geofysikk ,
eller (siden 1970-tallet) av og til som en kombinert "astro-gravimetrisk geoid".

Med metode (1) var avstandene mellom målepunktene mellom ca. 10 km og 50 km, avhengig av ønsket nøyaktighet (5 cm til 50 cm), med (2, 3) ca. 3 til 15 km. Den såkalte centimeter geoiden har strebet etter siden 1995 og har allerede oppnådd en nøyaktighet på 2 til 3 cm i noen sentraleuropeiske land.

Med den økende suksessen til satellittgeodesi bidro modeller av geopotensialet (gravitasjonsfelt i verdensrommet ) til geografisk bestemmelse. Fra orbitalforstyrrelsene forårsaket av geoiden og jordens indre ble det beregnet potensielle utviklinger av høy kvalitet med sfæriske overflatefunksjoner , som opprinnelig hadde en oppløsning på rundt 20 breddegrader og lengdegrader (rundt 1000 km × 1000 km), men nå allerede ned til 0,5 ° (rundt 50 km).

Den første sfæriske funksjonsutviklingen hadde globale nøyaktigheter på omtrent 10 m, som har forbedret seg til godt under 1 m (det er omtrent 0,00001% av jordens radius ). I motsetning til metodene nevnt ovenfor, kan de ikke løse noen detaljer, men de kan støtte en regional geoid til utsiden og gjøre fusjonen i stand til å danne kontinentale løsninger. Den siste metoden er satellitt-til-satellitt-sporing (STS).

litteratur

Christoph Reigber , Peter Schwintzer: Jordens gravitasjonsfelt. I: Fysikk i vår tid. 34 (5), 2003, ISSN 0031-9252 , s. 206-212.
Erwin Groten: Geodesi og jordens gravitasjonsfelt. Bind I: Prinsipper og konvensjonelle metoder. Bonn 1979.
Karl Ledersteger : Astronomisk og fysisk geodesi (= håndbok for oppmåling. Bind 5). 10. utgave, Metzler, Stuttgart 1969.
Gottfried Gerstbach : Hvordan få en europeisk centimeter geoid ("astro-geologisk geoid"). I: Jordens fysikk og kjemi. Volum 21/4. Elsevier, 1996, s. 343-346.
Heiner Denker, Jürgen Müller et al.: En ny kombinert høyde referanseoverflate for Tyskland ( GCG05 ). EUREF Conference, Riga 2006, ( plakat ; PDF; 414 kB).
Hans Sünkel , I. Marson (red.): Gravity and Geoid: Joint Symposium of the International Gravity Commission og International Geoid Commission. Konferansemøter september 1995 Graz (Østerrike). Springer 1996.
Mellomstatlig komité for kartlegging og kartlegging: Geosentrisk dato for Australia. Teknisk håndbok, versjon 2.2. ( PDF -fil , status: 2005).
Wolfgang Torge : Geodesi. 2. utgave, Walter de Gruyter, Berlin [et al.] 2003, ISBN 3-11-017545-2 .
Lieselotte Zenner: Analyse og sammenligning av forskjellige tyngdekraftfeltløsninger. I: Journal of Geodesy, Geoinformation and Land Management. 132. bind, nummer 3. Wißner, Augsburg 2007.

weblenker

Commons : Geoid - samling av bilder, videoer og lydfiler

Norbert Kühtreiber: High Precision Geoid Determination of Austria Using Heterogeneous Data ( Memento fra 21. august 2010 i Internettarkivet ) (Teori; PDF; 1,6 MB)
Stefan A. Voser: Geometriske krav til datautveksling
Konvertering mellom WGS84 referanse -ellipsoid og EGM96 geoid

Individuelle bevis

^ Axel Bojanowski : Jorden er en potet , Die Welt fra 1. august 2004.
^ Erwin Voellmy: Matematiske tabeller og formler. 17. utgave. Orell Füssli, Zürich 1973, ISBN 3-280-00682-1 , s. 159
↑ Den sesongbaserte poteten gfz-potsdam.de
^ Sesongmessige svingninger av den planetariske "poteten" målbare derstandard.at
↑ Jorden er en potet welt.de

[1] Axel Bojanowski : Jorden er en potet , Die Welt fra 1. august 2004.

[2] Erwin Voellmy: Matematiske tabeller og formler. 17. utgave. Orell Füssli, Zürich 1973, ISBN 3-280-00682-1 , s. 159

[3] Den sesongbaserte poteten gfz-potsdam.de

[4] Sesongmessige svingninger av den planetariske "poteten" målbare derstandard.at

[5] Jorden er en potet welt.de

[1]

[2]

[3]

[4]

[5]