Keplers lover

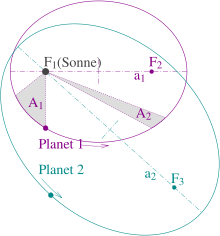
Grafisk oppsummering av de tre Kepler -lovene:
1. To elliptiske baner med solen i fokuspunktet F ₁ .
F ₂ og a ₁ er det andre fokuspunktet eller den store halvaksen for Planet1, F ₃ og ₂ for Planet2.
2. De to grå sektorene A ₁ og A ₂ , som har samme areal, blir feid over på samme tid.
3. Kvadratene til banetider på Planet1 og Planet2 oppfører seg som en ₁ ³ : a ₂ ³ .

De tre Kepler -lovene er de grunnleggende lovene for planetenes bane rundt solen. Johannes Kepler fant det på begynnelsen av 1600 -tallet da han prøvde å tilpasse det heliosentriske systemet i henhold til Copernicus til de nøyaktige astronomiske observasjonene til Tycho Brahe . På slutten av 1600-tallet var Isaac Newton i stand til å utlede Keplers lover i den klassiske mekanikken han grunnla som en eksakt løsning på tokroppsproblemet når det er en tiltrekning mellom de to kroppene som avtar med kvadratet på avstanden. Keplers lover er:

Første Keplers lov: Planetene beveger seg på elliptiske baner. Solen er i et av fokuspunktene.
Andre Keplers lov: En stråle trukket fra solen til planeten dekker områder av samme størrelse samtidig.
Tredje Keplers lov: De firkanter av banetider to planeter oppfører seg som kuber (tredje krefter ) av de store semiaxes av sine orbital ellipser .

Keplers lover gjelder for planetene i solsystemet til en god tilnærming. Avvikene i posisjonene på himmelen er vanligvis mindre enn ett vinkelminutt , dvs. ca. 1/30 fullmånediameter. De er kjent som orbitalforstyrrelser og er hovedsakelig basert på at planetene ikke bare tiltrekkes av solen, men også tiltrekker hverandre. Videre kan mye mindre korreksjoner beregnes i henhold til den generelle relativitetsteorien .

Keplers lover representerte et vesentlig skritt for å overvinne middelalderen til moderne vitenskap.De er av grunnleggende betydning i astronomi den dag i dag.

historie

Keplers utgangspunkt

Kepler var overbevist om det heliosentriske systemet til Copernicus (1543) fordi det var konseptuelt enklere og kom overens med færre antatte sirkler og parametere enn det geosentriske systemet til Ptolemaios, som hadde seiret fra omtrent 150 e.Kr. Det kopernikanske systemet muliggjorde også flere spørsmål, for for første gang var størrelsen på alle planetbaner i forhold til størrelsen på jordens bane klart definert her, uten å prøve ytterligere hypoteser. Kepler brukte livet på å lete etter en dypere forklaring på disse proporsjonene. På den tiden ble det også klart at planetene ikke kunne beveges av faste roterende krystallkuler på en gitt måte langs deres deferenter og episykler , fordi det ifølge Tycho Brahes observasjoner på kometen i 1577 burde ha trengt gjennom flere slike skjell. Tilsynelatende fant planetene veien gjennom rommet på egen hånd. Hastighetene deres, som kan bestemmes ut fra størrelsen på deres bane og deres bane tid, var i motsetning til de filosofisk baserte forutsetningene i det ptolemaiske systemet. Det var velkjent at de ikke forble konstant langs stien, men nå, i likhet med stienes form, krevde en ny forklaring. Alt dette motiverte Kepler til å ta det avgjørende skrittet i astronomien, til å anta "fysiske" årsaker til planetbevegelsen, det vil si de som allerede ble avslørt da de studerte jordiske bevegelser. Da motsatte han den fram til da hellige aristoteliske læren om en grunnleggende motsetning mellom himmel og jord og ga et viktig bidrag til den kopernikanske vending . ^[1]

For å undersøke dette mer presist, var det først nødvendig å bestemme planetenes faktiske baner. For dette formålet hadde Kepler tilgang til data fra Tychos tiår med himmelobservasjoner, som ikke bare var mye mer nøyaktige for første gang siden antikken (maksimal usikkerhet om to vinkelminutter), men også strakte seg over store deler av planetbanene. Ved evalueringen av disse dataene fulgte Kepler for første gang konsekvent det ledende prinsippet om at den fysiske årsaken til planetbevegelsene ligger i solen, og følgelig ikke i det fiktive punktet som kalles " midtsolen " (introdusert av Ptolemaios og plassert i det tomme midten av den sirkelen av Copernicus som han hadde tildelt jorden), men i den sanne fysiske solen. Han forestilte seg at solen virket på planetene som en magnet, og han utførte også dette bildet i detalj.

I sitt arbeid brøt Kepler også ny vei på andre måter. Som et utgangspunkt for analyse av banene, i motsetning til alle tidligere astronomer, tok han ikke den uniforme sirkelbevegelsen som filosofene foreskrev siden Platon og Aristoteles, som deretter ble lagt til ytterligere jevne sirkulære bevegelser for å forbedre korrespondansen med planetariske posisjoner observert på himmelen ( episyklisk teori ). Snarere prøvde han først å rekonstruere de faktiske banene og den variable hastigheten som planetene kjører på dem direkte fra himmelens observasjoner.

For det tredje brøt Kepler også ny vei i måten arbeidet hans ble presentert på. Frem til da var det vanlig at astronomer beskrev sitt syn på verden i en fullt utviklet tilstand. De forklarte hvordan de skulle bygge det opp stykke for stykke, og siterte filosofiske eller teologiske begrunnelser for hver av de nødvendige individuelle forutsetningene. Kepler, derimot, beskrev trinnvis den faktiske fremgangen i hans mangeårige arbeid, inkludert hans periodiske feil på grunn av uegnede tilnærminger. I 1609 publiserte han den første delen av resultatene hans som Astronomia Nova med det betydelige tillegg i tittelen (oversatt) "Ny astronomi, årsakssammenhengende eller himmelens fysikk, [...] i henhold til observasjonene fra adelsmannen Tycho Brahe ". Verket kulminerer i de to første Keplers lover, som hver gjelder for en enkelt planetbane. Keplers dypere forklaring på hele systemet og forholdet mellom planetbanene dukket opp i 1619 under tittelen Harmonices mundi ("Harmonies of the World"). Det er et forslag i det som senere ble kjent som Keplers tredje lov.

Keplers tilnærming

Keplers første resultat på jobben var at verken det ptolemaiske eller det kopernikanske systemet kunne gjengi planetstillingene med tilstrekkelig nøyaktighet, selv etter å ha forbedret individuelle parametere, f.eks. B. eksentrisitetene . Imidlertid fortsatte han å bruke disse modellene som en tilnærming for å velge fra Tychos observasjoner de som ville være best egnet for en mer presis karakterisering av banene. Så han fant ut at de eksentriske banene til Mars og jorden med hensyn til de faste stjernene forblir faste (med tilstrekkelig nøyaktighet), at hver kjører i et plan der solen er, og at de to bane -planene er litt skrå mot hverandre .

Dermed kunne Kepler anta at Mars, selv om dens eksakte bane fortsatt var ukjent, ville innta den samme posisjonen i rommet etter hver sin bane rundt solen, selv om den vises på forskjellige himmelske posisjoner sett fra jorden, fordi da jorden hver Noen ganger er den på et annet punkt i sin vei. Fra dette bestemte han først jordens bane med omtrent firesifret nøyaktighet. På dette grunnlaget evaluerte han de andre observasjonene av Mars, der avvikene fra en sirkelbane er mer uttalt enn i tilfelle av jorden. Da han etter mange feil og lange forsøk ikke klarte å trykke på den maksimale feilen på Mars posisjon på himmelen under åtte vinkelminutter (ca. 1/4 fullmånediameter), tok han et nytt forsøk og fant - halvparten ved en tilfeldighet - at Mars bane var best gjennom en Ellipse skal reproduseres, med solen i et av fokuspunktene. Dette resultatet ble også bekreftet med jordens bane, og det matchet også alle andre planeter observert av Tycho. Kepler visste at en elliptisk bane også kan sammensettes nøyaktig fra to sirkulære bevegelser, men han vurderte ikke denne muligheten ytterligere. For en nøyaktig fremstilling av bevegelsen må disse sirkulære bevegelsene løpe rundt sine respektive senterpunkter med variabel hastighet, og det er ingen fysisk årsak til det:

"Kepler gjorde ikke bruk av den epicykliske generasjonen av ellipsen fordi den ikke stemmer overens med de naturlige årsakene som produserer ellipsen [...]. " ^[2]

I det påfølgende søket etter loven om hele strukturen i solsystemet, som igjen varte i omtrent et tiår, forfulgte Kepler ideen om en harmoni som ligger til grunn for skapelsesplanen, som - som i tilfelle av harmoni i musikk - bør finnes i enkle numeriske forhold. Han publiserte resultatet i 1619 som Harmonice mundi ('Harmonies of the World'). For senere astronomi er bare den korte meldingen (i verkets femte bok) av varig verdi, ifølge hvilken kvadratene til alle planets omløpstid er i samme forhold som (med moderne ord) majorens tredje makter semiaxer av deres orbitale ellipser.

Kepler så også etter en fysisk forklaring på hvordan solen kunne virke på planetene for å forårsake de observerte bevegelsene. Hans refleksjoner om en magnetisk handling på avstand eller en anima motrix iboende på planetene, forble imidlertid resultatløse. Isaac Newton var senere i stand til å bevise at de tre Keplers lover reproduserer den nøyaktige løsningen av bevegelsen til et legeme under virkningen av en kraft i henhold til Newtons gravitasjonslov . Dette regnes som et betydelig skritt i utviklingen av klassisk mekanikk og moderne vitenskap som helhet. ^[3] ^[4] ^[5] ^[6]

Heliosentrisk og grunnleggende formulering av lovene

Kepler formulerte loven for planetene han kjente. For lovene gjelder imidlertid det kosmologiske prinsippet , siden de er gyldige overalt i universet .

Det heliosentriske tilfellet av solsystemet er imidlertid den desidert viktigste, og derfor er litteraturen ofte formulert restriktivt bare for planeter. De er selvfølgelig også gyldige for måner , asteroidebeltet og Oortskyen , eller ringene til Jupiter og Saturn , for stjerneklynger så vel som for objekter i bane rundt midten av en galakse , og for alle andre objekter i verdensrommet . De danner også grunnlaget for romfart og satellittbaner .

På kosmisk skala begynner de relativistiske effektene imidlertid å ha en økende effekt, og forskjellene til Kepler -modellen tjener først og fremst som et testkriterium for mer moderne begreper om astrofysikk. Dannelsesmekanismene i spiralgalakser, for eksempel, kan ikke lenger gjengis konsekvent med en modell som bare er basert på Keplers lover.

Avledning og moderne representasjon

Kepler prøvde å beskrive planetbevegelsene med sine lover. Fra de observerte verdiene, spesielt Mars bane, visste han at han måtte avvike fra idealet om sirkulære baner. I motsetning til Newtons senere teoretiske avledninger, er lovene hans derfor empiriske. Fra dagens synspunkt kan vi imidlertid starte med kunnskapen om Newtons gravitasjon og dermed begrunne gyldigheten av Keplers lover.

Keplers lover kan elegant stammer direkte fra Newtons bevegelsesteori.

Den første loven følger av Clairauts ligning , ^[7] som beskriver en komplett løsning av en bevegelse i rotasjonssymmetriske kraftfelt. ^[Åttende]

Den andre loven er en geometrisk tolkning av bevaringen av vinkelmomentet . ^[9]

Ved hjelp av integrasjon, Kepler -ligningen og den gaussiske konstanten følger den tredje loven fra den andre ^[10] eller ved hjelp av hodografen direkte fra Newtons lover. ^[11] I tillegg følger det i henhold til prinsippet om mekanisk likhet direkte fra gravitasjonskraftens inverse-kvadratiske avhengighet av avstanden. ^[12]

Første Keplers lov (teorem om ellipser)

Første Keplers lov

Bane til en satellitt er en ellipse . Et av fokuspunktene deres ligger i systemets tyngdepunkt .

Denne loven er et resultat av Newtons gravitasjonslov , forutsatt at massen til sentrallegemet er betydelig større enn satellittens og satellittens effekt på sentrallegemet kan neglisjeres.

Energien til en satellitt med masse $m$ ${\ displaystyle m}$ $m$ i det newtonske gravitasjonsfeltet til solen med masse $M.$ ${\ displaystyle M}$ $M.$ er i sylindriske koordinater

E=E_{\mathrm {kin} }+E_{\mathrm {pot} }={\frac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\phi }}^{2})-{\frac {GMm}{r}}.

{\ displaystyle E = E _ {\ mathrm {kin}} + E _ {\ mathrm {pot}} = {\ frac {1} {2}} m ({\ dot {r}} ^ {2} + r ^ {2} {\ dot {\ phi}} ^ {2}) - {\ frac {GMm} {r}}.}

E = E _ {{\ mathrm {kin}}} + E _ {{\ mathrm {pot}}} = {\ frac {1} {2}} m ({\ dot r} ^ {2} + r ^ {2} {\ dot \ phi} ^ {2}) - {\ frac {GMm} {r}}.

Ved hjelp av vinkelmoment $L=mr^{2}d\phi /dt$ ${\ displaystyle L = mr ^ {2} d \ phi / dt}$ $L = mr ^ {2} d \ phi / dt$ og

{\frac {dr}{dt}}={\frac {dr}{d\phi }}{\frac {d\phi }{dt}}\ \Rightarrow \ {\dot {r}}={\frac {dr}{d\phi }}{\dot {\phi }}

{\ displaystyle {\ frac {dr} {dt}} = {\ frac {dr} {d \ phi}} {\ frac {d \ phi} {dt}} \ \ Rightarrow \ {\ dot {r}} = {\ frac {dr} {d \ phi}} {\ dot {\ phi}}}

{\ frac {dr} {dt}} = {\ frac {dr} {d \ phi}} {\ frac {d \ phi} {dt}} \ \ Rightarrow \ {\ dot r} = {\ frac {dr } {d \ phi}} {\ dot \ phi}

tillater energilikningen

\left({\frac {dr}{d\phi }}\right)^{2}=2m{\frac {r^{4}}{L^{2}}}\left[E+{\frac {GMm}{r}}-{\frac {L^{2}}{2mr^{2}}}\right]

{\ displaystyle \ left ({\ frac {dr} {d \ phi}} \ right) ^ {2} = 2m {\ frac {r ^ {4}} {L ^ {2}}} \ left [E + {\ frac {GMm} {r}} - {\ frac {L ^ {2}} {2mr ^ {2}}} \ høyre]}

\ venstre ({\ frac {dr} {d \ phi}} \ høyre) ^ {2} = 2m {\ frac {r ^ {4}} {L ^ {2}}} \ venstre [E + {\ frac {GMm} {r}} - {\ frac {L ^ {2}} {2mr ^ {2}}} \ høyre]

omforme. Denne differensiallikningen brukes med den polare koordinatrepresentasjonen

r(\phi )={\frac {p}{1+\varepsilon \cdot \cos \phi }}

{\ displaystyle r (\ phi) = {\ frac {p} {1+ \ varepsilon \ cdot \ cos \ phi}}}

r (\ phi) = {\ frac {p} {1+ \ varepsilon \ cdot \ cos \ phi}}

av en kjeglesnitt. Dette gjøres ved å bruke derivatet

{\frac {dr}{d\phi }}={\frac {p\varepsilon \cdot \sin \phi }{(1+\varepsilon \cdot \cos \phi )^{2}}}

{\ displaystyle {\ frac {dr} {d \ phi}} = {\ frac {p \ varepsilon \ cdot \ sin \ phi} {(1+ \ varepsilon \ cdot \ cos \ phi) ^ {2}}}}

{\ frac {dr} {d \ phi}} = {\ frac {p \ varepsilon \ cdot \ sin \ phi} {(1+ \ varepsilon \ cdot \ cos \ phi) ^ {2}}}

dannet og alle uttrykk som $\phi$ ${\ displaystyle \ phi}$ $\ phi$ er inkludert ved å sette inn til

\varepsilon \cdot \cos \phi ={\frac {p}{r}}-1

{\ displaystyle \ varepsilon \ cdot \ cos \ phi = {\ frac {p} {r}} - 1}

\ varepsilon \ cdot \ cos \ phi = {\ frac {p} {r}} - 1

transformert ligning av banen elimineres:

{\frac {dr}{d\phi }}={\frac {r^{2}\varepsilon \cdot \sin \phi }{p}}\Rightarrow

{\ displaystyle {\ frac {dr} {d \ phi}} = {\ frac {r ^ {2} \ varepsilon \ cdot \ sin \ phi} {p}} \ Rightarrow}

{\ frac {dr} {d \ phi}} = {\ frac {r ^ {2} \ varepsilon \ cdot \ sin \ phi} {p}} \ Høyre pil

\left({\frac {dr}{d\phi }}\right)^{2}={\frac {r^{4}\varepsilon ^{2}(1-\cos ^{2}\phi )}{p^{2}}}={\frac {r^{4}}{p^{2}}}\left(\varepsilon ^{2}-\left({\frac {p}{r}}-1\right)^{2}\right)={\frac {r^{4}}{p^{2}}}\left(\varepsilon ^{2}-1+{\frac {2p}{r}}-{\frac {p^{2}}{r^{2}}}\right)\Rightarrow

{\ displaystyle \ left ({\ frac {dr} {d \ phi}} \ right) ^ {2} = {\ frac {r ^ {4} \ varepsilon ^ {2} (1- \ cos ^ {2} \ phi)} {p ^ {2}}} = {\ frac {r ^ {4}} {p ^ {2}}} \ venstre (\ varepsilon ^ {2} - \ venstre ({\ frac {p} {r}} - 1 \ høyre) ^ {2} \ høyre) = {\ frac {r ^ {4}} {p ^ {2}}} \ venstre (\ varepsilon ^ {2} -1 + {\ frac {2p} {r}} - {\ frac {p ^ {2}} {r ^ {2}}} \ right) \ Rightarrow}

\ venstre ({\ frac {dr} {d \ phi}} \ høyre) ^ {2} = {\ frac {r ^ {4} \ varepsilon ^ {2} (1- \ cos ^ {2} \ phi) } {p ^ {2}}} = {\ frac {r ^ {4}} {p ^ {2}}} \ venstre (\ varepsilon ^ {2} - \ venstre ({\ frac {p} {r} } -1 \ right) ^ {2} \ right) = {\ frac {r ^ {4}} {p ^ {2}}} \ left (\ varepsilon ^ {2} -1 + {\ frac {2p} {r}} - {\ frac {p ^ {2}} {r ^ {2}}} \ høyre) \ Høyre pil

p={\frac {({\frac {L}{m}})^{2}}{GM}}{\text{ und }}\varepsilon ={\sqrt {1+{\frac {2{\frac {E}{m}}({\frac {L}{m}})^{2}}{G^{2}M^{2}}}}}

{\ displaystyle p = {\ frac {({\ frac {L} {m}}) ^ {2}} {GM}} {\ text {og}} \ varepsilon = {\ sqrt {1 + {\ frac { 2 {\ frac {E} {m}} ({\ frac {L} {m}}) ^ {2}} {G ^ {2} M ^ {2}}}}}}

p = {\ frac {({\ frac {L} {m}}) ^ {2}} {GM}} {\ text {og}} \ varepsilon = {\ sqrt {1 + {\ frac {2 {\ frac {E} {m}} ({\ frac {L} {m}}) ^ {2}} {G ^ {2} M ^ {2}}}}}

ved å sammenligne koeffisientene til makten til $r .$ ${\ displaystyle r.}$ ${\ displaystyle r.}$

Denne løsningen avhenger bare av den spesifikke energien $E/m$ ${\ displaystyle E / m}$ $E / m$ og den spesifikke orbitale vinkelmomentet $L/m$ ${\ displaystyle L / m}$ $L / m$ borte. Parameteren $s$ ${\ displaystyle p}$ $s$ og den numeriske eksentrisiteten $\varepsilon$ ${\ displaystyle \ varepsilon}$ $\ varepsilon$ er designelementene i jernbanen . I tilfellet $0<\varepsilon <1\,(E<0)$ ${\ displaystyle 0 <\ varepsilon <1 \, (E <0)}$ $0 <\ varepsilon <1 \, (E <0)$ gjelder:

{\text{Der durch }}r(\phi ){\text{ beschriebene Kegelschnitt ist eine Ellipse.}}

{\ displaystyle {\ text {Den koniske delen beskrevet av}} r (\ phi) {\ text {er en ellipse.}}}

{\ text {Den koniske delen beskrevet av}} r (\ phi) {\ text {er en ellipse.}}

... først Keplers lov

Beskrivelse av ellipsen
Stor halvakse	$a={\frac {p}{1-\varepsilon ^{2}}}$ ${\ displaystyle a = {\ frac {p} {1- \ varepsilon ^ {2}}}}$ ${\ displaystyle a = {\ frac {p} {1- \ varepsilon ^ {2}}}}$
Liten halvakse	$b={\frac {p}{\sqrt {1-\varepsilon ^{2}}}}$ ${\ displaystyle b = {\ frac {p} {\ sqrt {1- \ varepsilon ^ {2}}}}}$ ${\ displaystyle b = {\ frac {p} {\ sqrt {1- \ varepsilon ^ {2}}}}}$
Foci	$F_{1}=(0,0)$ ${\ displaystyle F_ {1} = (0,0)}$ $F_ {1} = (0.0)$ $F_{2}=\left(-{\frac {2\varepsilon p}{1-\varepsilon ^{2}}},0\right)$ ${\ displaystyle F_ {2} = \ left (- {\ frac {2 \ varepsilon p} {1- \ varepsilon ^ {2}}}, 0 \ right)}$ ${\ displaystyle F_ {2} = \ left (- {\ frac {2 \ varepsilon p} {1- \ varepsilon ^ {2}}}, 0 \ right)}$
Pericenter	$P=\left(r_{\mathrm {min} }={\frac {p}{1+\varepsilon }},0\right)$ ${\ displaystyle P = \ left (r _ {\ mathrm {min}} = {\ frac {p} {1+ \ varepsilon}}, 0 \ right)}$ ${\ displaystyle P = \ left (r _ {\ mathrm {min}} = {\ frac {p} {1+ \ varepsilon}}, 0 \ right)}$
Apocenter	$A=\left(-r_{\mathrm {max} }=-{\frac {p}{1-\varepsilon }},0\right)$ ${\ displaystyle A = \ left (-r _ {\ mathrm {max}} =- {\ frac {p} {1- \ varepsilon}}, 0 \ right)}$ ${\ displaystyle A = \ left (-r _ {\ mathrm {max}} =- {\ frac {p} {1- \ varepsilon}}, 0 \ right)}$

To kropper kretser rundt sitt felles tyngdepunkt -
her idealiserte sirkelbaner som en spesiell form på ellipsen

Hvis man (i motsetning til Kepler) ikke tar et sentralt symmetrisk kraftfelt som grunnlag, men i stedet gjensidig virkende gravitasjon, dannes det også elliptiske baner. Begge legemer beveger seg, men banen i midten er det felles tyngdepunktet for "sentrallegemet" og Trabant, den totale massen av systemet må antas som den fiktive sentrale massen. Imidlertid er det felles tyngdepunktet til solsystemets planeter og solen (solsystemet barycenter) fortsatt i solen: Solen hviler ikke i forhold til den, men svinger litt under påvirkning av planetene i bane ( lengden på solen ≠ 0). Jord-månesystemet , derimot, viser større svingninger når det gjelder bane-geometrien, også her er tyngdepunktet fortsatt innenfor jorden. Satellitter reagerer til og med på svingninger i kraftfeltet, som er uregelmessig på grunn av jordens form .

Selv om Keplers lover opprinnelig bare ble formulert for gravitasjonskraften, gjelder ovennevnte løsning også for Coulomb -styrken . For ladninger som frastøter hverandre, er det effektive potensialet da alltid positivt, og bare hyperboliske baner oppnås.

til $1/r^{2}$ ${\ displaystyle 1 / r ^ {2}}$ $1 / r ^ {2}$ Krefter, det er også en bevart mengde som er avgjørende for retningen til elliptisk bane, Runge-Lenz-vektoren , som peker langs hovedaksen. Små endringer i kraftfeltet (vanligvis på grunn av påvirkning fra de andre planetene) lar denne vektoren sakte endre retning. B. periheliet i Merkurius bane kan forklares.

Andre Keplers lov (områdesetning)

Andre Keplers lov

Samtidig fjerner fjernlyset objektet - tyngdepunktet over de samme områdene.

Fjernlyset er linjen som forbinder tyngdepunktet til et himmellegeme , f.eks. B. en planet eller måne, og tyngdepunktet , z. B. i en første tilnærming til solen eller planeten den beveger seg rundt.

Illustrasjon for å utlede områdesettet fra et lite tidstrinn

En enkel avledning oppnås hvis man ser på områdene som fjernlyset dekker på en liten periode. I grafikken til høyre er Z sentrum av kraften. Trabant beveger seg opprinnelig fra A til B. Hvis hastigheten ikke endret seg, ville den gå fra B til C i neste trinn. Det kan raskt sees at de to trekantene ZAB og ZBC inneholder det samme området. Hvis en kraft nå virker i retning Z, vil hastigheten være $v$ ${\ displaystyle v}$ $v$ rundt a $\Delta v$ ${\ displaystyle \ Delta v}$ $\ Delta v$ avbøyd, som er parallell med den felles basen ZB for de to trekanter. I stedet for C lander Trabant på C '. Siden de to trekanter ZBC og ZBC 'har samme base og samme høyde, er området også det samme. Områdesetningen gjelder de to små tidssegmentene $[-\Delta t,0]$ ${\ displaystyle [- \ Delta t, 0]}$ $[- \ Delta t, 0]$ og $[0,\Delta t]$ ${\ displaystyle [0, \ Delta t]}$ $[0, \ Delta t]$ . Hvis man integrerer slike små tidstrinn (med uendelige tidstrinn $\Delta t$ ${\ displaystyle \ Delta t}$ $\ Delta t$ ), får vi områdesetningen.

Det feide området er for et uendelig minimalt tidstrinn

F(t,t+\operatorname {d} t)=1/2|\mathbf {r} (t)\times \mathbf {\dot {r}} (t)\operatorname {d} t|={\frac {L}{2m}}\operatorname {d} t

{\ displaystyle F (t, t + \ operatorname {d} t) = 1/2 | \ mathbf {r} (t) \ times \ mathbf {\ dot {r}} (t) \ operatorname {d} t | = {\ frac {L} {2m}} \ operatornavn {d} t}

F (t, t + \ operatorname {d} t) = 1/2 | {\ mathbf {r}} (t) \ times {\ mathbf {{\ dot r}}} (t) \ operatorname {d} t | = {\ frac {L} {2m}} \ operatorname {d} t

.

Siden vinkelmomentet skyldes en sentral kraft

\mathbf {\dot {L}} =m(\mathbf {\dot {r}} \times \mathbf {\dot {r}} +\mathbf {r} \times \mathbf {\ddot {r}} )=m\mathbf {r} \times \mathbf {\ddot {r}} =m\mathbf {r} \times f(r)\mathbf {r} =0

{\ displaystyle \ mathbf {\ dot {L}} = m (\ mathbf {\ dot {r}} \ times \ mathbf {\ dot {r}} + \ mathbf {r} \ times \ mathbf {\ ddot {r }}) = m \ mathbf {r} \ times \ mathbf {\ ddot {r}} = m \ mathbf {r} \ ganger f (r) \ mathbf {r} = 0}

{\ displaystyle \ mathbf {\ dot {L}} = m (\ mathbf {\ dot {r}} \ times \ mathbf {\ dot {r}} + \ mathbf {r} \ times \ mathbf {\ ddot {r }}) = m \ mathbf {r} \ times \ mathbf {\ ddot {r}} = m \ mathbf {r} \ ganger f (r) \ mathbf {r} = 0}

er konstant, er området integrert rett

F(t_{0},t)={\frac {1}{2}}\int _{t_{0}}^{t}|\mathbf {r} (\tau )\times \mathbf {\dot {r}} (\tau )|\operatorname {d} \tau ={\frac {1}{2}}{\frac {L}{m}}\int _{t_{0}}^{t}\operatorname {d} \tau ={\frac {1}{2}}{\frac {L}{m}}(t-t_{0})

{\ displaystyle F (t_ {0}, t) = {\ frac {1} {2}} \ int _ {t_ {0}} ^ {t} | \ mathbf {r} (\ tau) \ times \ mathbf {\ dot {r}} (\ tau) | \ operatorname {d} \ tau = {\ frac {1} {2}} {\ frac {L} {m}} \ int _ {t_ {0}} ^ {t} \ operatorname {d} \ tau = {\ frac {1} {2}} {\ frac {L} {m}} (t-t_ {0})}

F (t_ {0}, t) = {\ frac {1} {2}} \ int _ {{t_ {0}}} ^ {t} | {\ mathbf r} (\ tau) \ times {\ mathbf {{\ dot r}}} (\ tau) | \ operatorname {d} \ tau = {\ frac {1} {2}} {\ frac {L} {m}} \ int _ {{t_ {0} }} ^ {t} \ operatorname {d} \ tau = {\ frac {1} {2}} {\ frac {L} {m}} (t-t_ {0})

.

For like tidsforskjeller $t-t_{0}$ ${\ displaystyle t-t_ {0}}$ ${\ displaystyle t-t_ {0}}$ Resultatet er det samme feide området.

Den andre Kepler -loven definerer både det geometriske grunnlaget for en astrometrisk bane (som en bane i et plan) og dens bane dynamikk (atferden over tid). Kepler formulerte loven bare for planetenes bane rundt solen, men den gjelder også for ikke-lukkede baner . I motsetning til de to andre lovene, er Keplers andre lov ikke basert på $1/r^{2}$ ${\ displaystyle 1 / r ^ {2}}$ $1 / r ^ {2}$ - Tyngdekraften begrenset (faktisk gikk Kepler også fra en med sin anima motrix $1/r$ ${\ displaystyle 1 / r}$ $1 / r$ -Force off), men gjelder generelt for alle sentrale krefter og bevegelser med konstant vinkelmoment. Kepler var bare interessert i en beskrivelse av planetbanene, men den andre loven er allerede den første formuleringen av loven som vi i dag kjenner som bevaring av vinkelmoment . Den andre Kepler -loven kan sees på som en spesiell formulering av vinkelsporteoremet, se også loven om virvel # overflatesetning .

Keplers andre lov har også to grunnleggende konsekvenser for bevegelsesforholdene i flerkroppssystemer , både for solsystemer og for romfart: Konstansen til bane normalvektor betyr at elementær himmelsk mekanikk er et flatt problem. Faktisk er det også avvik her på grunn av volumene til himmellegemene, slik at massen ligger utenfor baneplanet og planene til baneforløpet (endre posisjonen i rommet). Derfor ligger planetenes baner ikke alle i ett plan (det ideelle solsystemplanet, ekliptikken ), de viser heller en helning og også perihelionrotasjon , og solens ekliptiske breddegrad svinger også. Motsatt er det relativt enkelt å flytte et romfartøy i planet til solsystemet, men det er ekstremt komplekst, for eksempel å plassere en sonde over solens nordpol.

Overflathastighetens konstantitet betyr at en imaginær forbindelseslinje mellom sentrallegemet, nærmere bestemt tyngdepunktet til de to himmellegemene, og en satellitt alltid feier over det samme området samtidig. Så en kropp beveger seg raskere når den er i nærheten av tyngdepunktet og jo saktere jo lenger den er fra den. Dette gjelder for eksempel jordens forløp rundt solen så vel som månens gang eller en satellitt rundt jorden. En sti presenterer seg som et konstant fritt fall , som svinger nær tyngdepunktet og stiger igjen til det lengste kulminasjonspunktet på stien: Kroppen blir raskere og raskere, har den høyeste hastigheten i perisenteret (punktet nærmest sentrum ) og blir deretter langsommere og langsommere til apocenteret (det fjerneste punktet) som det akselererer igjen. Sett på denne måten er Keplerellipse et spesielt tilfelle av det skjeve kastet som stenger i bane. Denne vurderingen spiller en sentral rolle i romfysikken, hvor det gjelder å generere en passende bane med en passende valgt innledende impuls (gjennom starten): jo mer sirkulær bane, jo mer jevn banehastighet.

Tredje Keplers lov

Representasjon av forholdet mellom orbitalradius og orbitalperiode

Firkantene i syklustiden

T_{1}

${\ displaystyle T_ {1}}$ $T_ {1}$ og

T_{2}

${\ displaystyle T_ {2}}$ $T_ {2}$ Alle to satellitter rundt et felles senter er proporsjonale med tredjemaktene til de store semiaxene

a_{1}

${\ displaystyle a_ {1}}$ $a_ {1}$ og

a_{2}

${\ displaystyle a_ {2}}$ $a_2$ deres elliptiske baner.

eller

Kvadratene i revolusjonsperioden er i samme forhold som terningene (tredjemaktene) til de store semiaxene:

\left({\frac {T_{1}}{T_{2}}}\right)^{2}=\left({\frac {a_{1}}{a_{2}}}\right)^{3}

{\ displaystyle \ left ({\ frac {T_ {1}} {T_ {2}}} \ right) ^ {2} = \ left ({\ frac {a_ {1}} {a_ {2}}} \ høyre) ^ {3}}

\ venstre ({\ frac {T_ {1}} {T_ {2}}} \ høyre) ^ {2} = \ venstre ({\ frac {a_ {1}} {a_ {2}}} \ høyre) ^ {3}

... tredje Keplers lov

Kepler brukte for halve baneøksene $a_{1,2}$ ${\ displaystyle a_ {1,2}}$ $a _ {{1,2}}$ gjennomsnittlige avstander fra solen (når det gjelder gjennomsnittet av perihelion -avstand og apheld -avstand ).

C={\frac {T^{2}}{a^{3}}}

{\ displaystyle C = {\ frac {T ^ {2}} {a ^ {3}}}}

C = {\ frac {T ^ {2}} {a ^ {3}}}

... tredje Keplers lov, masseuavhengig formulering med Keplers konstant av sentralmassen ( Gauss-gravitasjonskonstant i solsystemet)

I kombinasjon med gravitasjonsloven er den tredje loven gitt av Kepler for bevegelse av to masser $M.$ ${\ displaystyle M}$ $M.$ og $m$ ${\ displaystyle m}$ $m$ skjema

T^{2}={\frac {4\pi ^{2}}{G(M+m)}}\cdot a^{3}\approx {\frac {4\pi ^{2}}{GM}}\cdot a^{3}

{\ displaystyle T ^ {2} = {\ frac {4 \ pi ^ {2}} {G (M + m)}} \ cdot a ^ {3} \ approx {\ frac {4 \ pi ^ {2} } {GM}} \ cdot a ^ {3}}

T ^ {2} = {\ frac {4 \ pi ^ {2}} {G (M + m)}} \ cdot a ^ {3} \ approx {\ frac {4 \ pi ^ {2}} {GM }} \ cdot a ^ {3}

... tredje Keplers lov, formulering med to masser

Tilnærmingen gjelder hvis massen $m$ ${\ displaystyle m}$ $m$ ubetydelig liten i forhold til $M.$ ${\ displaystyle M}$ $M.$ er (f.eks. i solsystemet). Med denne formen kan man bestemme den totale massen av binære stjernesystemer fra måling av revolusjonsperioden og avstanden.

Tatt i betraktning de forskjellige massene av to himmellegemer og formelen ovenfor, er en mer eksakt formulering av Keplers tredje lov:

\left({\frac {T_{1}}{T_{2}}}\right)^{2}=\left({\frac {a_{1}}{a_{2}}}\right)^{3}{\frac {M+m_{2}}{M+m_{1}}}

{\ displaystyle \ left ({\ frac {T_ {1}} {T_ {2}}} \ right) ^ {2} = \ left ({\ frac {a_ {1}} {a_ {2}}} \ høyre) ^ {3} {\ frac {M + m_ {2}} {M + m_ {1}}}}

\ venstre ({\ frac {T_ {1}} {T_ {2}}} \ høyre) ^ {2} = \ venstre ({\ frac {a_ {1}} {a_ {2}}} \ høyre) ^ {3} {\ frac {M + m_ {2}} {M + m_ {1}}}

... tredje Keplers lov, formulering med tre masser

Avviket får tydeligvis bare betydning hvis begge satellittene er veldig forskjellige i massene og det sentrale objektet har en masse $M.$ ${\ displaystyle M}$ $M.$ som ikke skiller seg veldig fra den til en av de to satellittene.

Den tredje Kepler lov gjelder for alle krefter som avtar kvadratisk med avstanden, som man lett kan utlede fra den skala betraktning. I ligningen

m{\frac {d^{2}r}{(dt)^{2}}}={\frac {GMm}{r^{2}}}

{\ displaystyle m {\ frac {d ^ {2} r} {(dt) ^ {2}}} = {\ frac {GMm} {r ^ {2}}}}

m {\ frac {d ^ {2} r} {(dt) ^ {2}}} = {\ frac {GMm} {r ^ {2}}}

dykk $r$ ${\ displaystyle r}$ $r$ i tredje makt og $t$ ${\ displaystyle t}$ $t$ firkant på. Under en skala transformasjon $r'=\alpha r,t'=\beta t$ ${\ displaystyle r '= \ alfa r, t' = \ beta t}$ $r '= \ alfa r, t' = \ beta t$ man får dermed den samme ligningen hvis $\alpha ^{3}=\beta ^{2}$ ${\ displaystyle \ alpha ^ {3} = \ beta ^ {2}}$ ${\ displaystyle \ alpha ^ {3} = \ beta ^ {2}}$ er. Andererseits ist dadurch schnell erkennbar, dass das Analogon des dritten Keplerschen Gesetzes für geschlossene Bahnen in einem $1/r^{k}$ $1/r^{k}$ $1/r^{k}$ -Kraftfeld für beliebiges $k$ ${\displaystyle k}$ $k$ gerade $(a_{1}/a_{2})^{k+1}=(T_{1}/T_{2})^{2}$ $(a_{1}/a_{2})^{k+1}=(T_{1}/T_{2})^{2}$ $(a_{1}/a_{2})^{{k+1}}=(T_{1}/T_{2})^{2}$ lautet. ^[13]

Siehe auch

Hohmann-Transfer , die Verbindungsbahn zweier Keplerbahnen der Raumfahrt
Spezifischer Drehimpuls , relativ einfache Herleitung der Keplerschen Gesetze ausgehend von der Drehimpulserhaltung

Literatur

Johannes Kepler: Astronomia nova aitiologetos seu Physica coelestis . In: Max Caspar (Hrsg.): Gesammelte Werke . Band 3 . CH Beck, München 1938.
Johannes Kepler: Harmonices Mundi libri V . In: Max Caspar (Hrsg.): Gesammelte Werke . Band 6 . CH Beck, München 1990, ISBN 3-406-01648-0 .
Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung . BI-Wiss.-Verlag, Mannheim 1994, ISBN 3-411-17051-4 .

Weblinks

Commons : Keplersche Gesetze – Sammlung von Bildern, Videos und Audiodateien

Walter Fendt: 1. Keplersches Gesetz , 2. Keplersches Gesetz (HTML5-Apps).
Keplersche Gesetze ( LEIFI ).
Joachim Hoffmüller: 2. Keplersches Gesetz (Flächensatz): Beweis mit dynamischen Arbeitsblättern selbst nachvollziehen. Geometrisch-anschaulicher Beweis nach Newton, ohne höhere Mathematik ( Java-Applet ).
Video: Keplersche Gesetze der Planetenbewegungen . Institut für den Wissenschaftlichen Film (IWF) 1978, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi : 10.3203/IWF/C-1286 .

Einzelnachweise

↑ Thomas S. Kuhn: Die Kopernikanische Revolution. Vieweg, Braunschweig 1980, ISBN 3-528-08433-2 .
↑ Carl B. Boyer: Note on Epicycles & the Ellipse from Copernicus to Lahire . In: Isis . Band 38 , 1947, S. 54–56 . Der hier kursiv zitierte Satz von Kepler ist dort als direkte Übersetzung wiedergegeben.
↑ Arthur Koestler: Die Nachtwandler: Die Entstehungsgeschichte unserer Welterkenntnis . Suhrkamp, 1980.
↑ Bruce Stephenson: Kepler's physical astronomy . Springer Science & Business Media Bd. 13, 2012.
↑ Martin Holder: Die Kepler-Ellipse . universi, Siegen 2015 ( online [PDF; abgerufen am 1. November 2017]).
↑ Curtis Wilson: How Did Kepler Discover His First Two Laws? In: Scientific American . Band 226 , Nr. 3 , 1972, S. 92–107 , JSTOR : 24927297 .
↑ Guthmann, § II.2.37 Lösung der Clairotschen Gleichung: Der Fall e<1. S. 81 f.
↑ Guthmann, § II.1 Ein- und Zweikörperproblem. Einführung, S. 64 f. und 30. Die Clairotsche Gleichung. S. 71 ff.
↑ Guthmann, § II.1.26 Der Flächensatz. S. 66 f.
↑ Guthmann, § II.5 Bahndynamik des Keplerproblems. S. 108 ff.
↑ David L. Goodstein, Judith R. Goodstein: Feynmans verschollene Vorlesung: Die Bewegung der Planeten um die Sonne . Piper Verlag GmbH, München 1998.
↑ LD Landau und EM Lifshitz: Mechanics . 3. Auflage. Butterworth-Heinemann, Oxford 1976, ISBN 978-0-7506-2896-9 , S. 22–24 (englisch).
↑ J. Wess: Theoretische Mechanik. Springer. Kapitel über das Zweikörperproblem.

[1] Thomas S. Kuhn: Die Kopernikanische Revolution. Vieweg, Braunschweig 1980, ISBN 3-528-08433-2 .

[Boyer1947-2] Carl B. Boyer: Note on Epicycles & the Ellipse from Copernicus to Lahire . In: Isis . Band 38 , 1947, S. 54–56 . Der hier kursiv zitierte Satz von Kepler ist dort als direkte Übersetzung wiedergegeben.

[Koestler-3] Arthur Koestler: Die Nachtwandler: Die Entstehungsgeschichte unserer Welterkenntnis . Suhrkamp, 1980.

[Stephenson-4] Bruce Stephenson: Kepler's physical astronomy . Springer Science & Business Media Bd. 13, 2012.

[Holder2015-5] Martin Holder: Die Kepler-Ellipse . universi, Siegen 2015 ( online [PDF; abgerufen am 1. November 2017]).

[Wilson1972-6] Curtis Wilson: How Did Kepler Discover His First Two Laws? In: Scientific American . Band 226 , Nr. 3 , 1972, S. 92–107 , JSTOR : 24927297 .

[Guth_37-7] Guthmann, § II.2.37 Lösung der Clairotschen Gleichung: Der Fall e<1. S. 81 f.

[Guth_Cl-8] Guthmann, § II.1 Ein- und Zweikörperproblem. Einführung, S. 64 f. und 30. Die Clairotsche Gleichung. S. 71 ff.

[Guth_26-9] Guthmann, § II.1.26 Der Flächensatz. S. 66 f.

[Guth_#5-10] Guthmann, § II.5 Bahndynamik des Keplerproblems. S. 108 ff.

[11] David L. Goodstein, Judith R. Goodstein: Feynmans verschollene Vorlesung: Die Bewegung der Planeten um die Sonne . Piper Verlag GmbH, München 1998.

[12] LD Landau und EM Lifshitz: Mechanics . 3. Auflage. Butterworth-Heinemann, Oxford 1976, ISBN 978-0-7506-2896-9 , S. 22–24 (englisch).

[13] J. Wess: Theoretische Mechanik. Springer. Kapitel über das Zweikörperproblem.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[Åttende]

[9]

[10]

[11]

[12]

[13]