Funksjon (matematikk)
I matematikk er en funksjon ( latinsk functio ) eller kartlegging et forhold ( forhold ) mellom to sett , som tilsvarer hvert element i det ene settet (funksjonsargument, uavhengig variabel, Verdi) nøyaktig ett element i det andre settet (funksjonsverdi, avhengig variabel, Verdi). Begrepet funksjon er definert annerledes i litteraturen, men man starter vanligvis fra ideen om at funksjoner tildeler matematiske objekter til matematiske objekter, for eksempel hvert virkelige tall er kvadratet. Begrepet funksjon eller kartlegging inntar en sentral posisjon i moderne matematikk; Som spesialtilfeller inneholder den blant annet parametriske kurver , skalar- og vektorfelt ,transformasjoner , operasjoner , operatører og mye mer.
Konsepthistorie
De første tilnærmingene til en implisitt bruk av det funksjonelle uttrykket i tabellform (skyggelengde avhengig av tidspunktet på dagen, akkordlengde avhengig av sentralvinkelen, etc.) kan allerede sees i antikken. Det første beviset på en eksplisitt definisjon av funksjonsbegrepet kan bli funnet hos Nikolaus von Oresme , som på 1300 -tallet grafisk representerte avhengighetene til endrede mengder (varme, bevegelse osv.) Ved hjelp av vinkelrette linjer (longitudo, latitudo) . [1] I begynnelsen av prosessen med å utvikle funksjonsbegrepet er Descartes og Fermat , som utviklet den analytiske metoden for å introdusere funksjoner ved hjelp av variablene som ble introdusert av Vieta . [2] Funksjonelle avhengigheter bør representeres av ligninger som f.eks å være representert. I skolematematikk ble dette naive funksjonskonseptet beholdt langt inn i andre halvdel av 1900 -tallet. Den første beskrivelsen av funksjonsbegrepet basert på denne ideen kommer fra Gregory i boken Vera circuli et hyperbolae quadratura , utgitt i 1667 . Begrepet funksjon dukket sannsynligvis først opp i 1673 i et manuskript av Leibniz , som også brukte begrepene "konstant", "variabel", "ordinat" og "abscissa" i sin avhandling De linea ex lineis numero infinitis ordinatim ductis fra 1692 . I korrespondansen mellom Leibniz og Johann I Bernoulli er funksjonsbegrepet løsrevet fra geometri og overført til algebra. Bernoulli beskriver denne utviklingen i bidrag fra 1706, 1708 og 1718. I 1748 forbedret Leonhard Euler , elev av Johann Bernoulli, funksjonsbegrepet i sin bok Introductio in analysin infinitorum . [3]
Euler har to forskjellige forklaringer på funksjonsbegrepet: På den ene siden setter alle "analytiske uttrykk" inn en funksjon blir en annen definert i koordinatsystemet med en frihåndstegnet kurve. [4] I 1755 omformulerte han disse ideene uten å bruke begrepet "analytisk uttrykk". Han brukte også stavemåten allerede i 1734 på. Han skiller mellom unike og tvetydige funksjoner. Med Euler er inversjonen av den normale parabelen , der hvert ikke-negative reelle tall er tildelt både den positive og den negative roten, tillatt som en funksjon. For Lagrange er bare funksjoner tillatt som er definert av kraftserier, slik han uttalte i sin Théorie des fonctions analytiques i 1797. En fruktbar diskusjon om bevegelsesloven for en vibrerende streng, som d'Alembert i 1747, Euler 1748 og Daniel Bernoulli presenterte forskjellige løsninger i 1753, førte til oppdagelsen av definisjonssettet og et mer presist funksjonsbegrep, i som noe som en klar oppgave allerede er beskrevet Fourier i boken Théorie analytique de la chaleur fra 1822 . Cauchy formulerte noe lignende i 1823 i Résumé des leçons ... sur le calcul infinitésimal.
Da analyse ble plassert på et nytt grunnlag med et eksakt grenseverdi -konsept på 1800 -tallet, ble eiendommer som tidligere ble forstått som konstituerende funksjoner introdusert som uavhengige begreper i en eksakteringsprosess og atskilt fra funksjonskonseptet. Dirichlet , en student av Fourier, formulerte dette nye synet: "Ideer i stedet for regninger" og presenterte ideene sine i 1837. Stokes utførte lignende synspunkter i verk i 1848 og 1849. Slik fortsatte Riemann , en elev av Dirichlet, i 1851 i grunnlaget for en generell teori om funksjonene til en variabel kompleks mengde med kontinuitet, senere fulgte integritet og differensiering. Hankel oppsummerte denne utviklingen i 1870 i sine undersøkelser av de uendelig ofte oscillerende og diskontinuerlige funksjonene. Igjen er det fortsatt ingen mellom funksjonen og funksjonsverdien på poenget differensiert. [5]
Weierstraß , Dedekind og andre oppdaget at grenseverdier for uendelige sekvenser av "klassiske" funksjoner kan være uberegnelige og ikke alltid kan uttrykkes med "lukkede" formler, dvs. med et begrenset antall aritmetiske operasjoner. Dette tvang til en gradvis utvidelse av funksjonsbegrepet.
Uavhengig av dette ble gruppeteorien grunnlagt på 1800 -tallet, som man systematisk kan undersøke hvordan algebraiske ligninger endres under effekten av påfølgende transformasjoner. Når vi brukte denne teorien på geometriske problemer, ble begrepene bevegelse og kartlegging brukt synonymt med transformasjon .
Da grunnleggende matematikk ble enhetlig formulert på språket i setteteorien på begynnelsen av 1900 -tallet, viste de matematiske begrepene funksjon og kartlegging seg å være kongruente. Imidlertid har de forskjellige tradisjonene fortsatt en effekt på språkbruken. I analysen i dag snakker man ofte om funksjoner, mens man i algebra og geometri snakker om kartlegginger. Selv i dag skiller noen matematikere et strengt skille mellom en kartlegging og en funksjon. Disse forstår en funksjon som en kartlegging i det virkelige eller komplekse tallfeltet ( eller. ) eller også potensene derav ( eller. ), på den annen side er det vanlig i boolsk algebra å snakke om boolske funksjoner .
Andre synonymer for funksjon i mer spesifikke sammenhenger inkluderer operatører innen analyse, drift, kobling og (noe generalisert) morfisme i algebra.
I dag anser noen forfattere at funksjonsbegrepet (så vel som det relasjonelle konseptet) ikke nødvendigvis er beløp begrenset til, men la hver av bestilte par eksisterende klasse som ikke inneholder forskjellige elementer med den samme venstre komponenten, betraktes som funksjonell. [6] [7] Uttrykt i settteori, er funksjoner definert som rett-entydige relasjoner .
definisjon
Grunnleggende idé
En funksjon tildeler hvert element et definisjonssett nøyaktig ett element et målsett til.
Notasjon:
- , eller tilsvarende:
For elementet det tildelte elementet i målsettingen er vanligvis skrevet .
Merknader:
- Det motsatte gjelder ikke: et element i målsett kan tildeles nøyaktig ett, flere, men heller ikke noe element i definisjonssettet, i så fall tilhører det ikke bildesettet . [Åttende]
Eksempel: beløpsfunksjonen tilordner tallene +1 og −1 i definisjonssettet til tallet +1 til målesettet. Tallet +1 for målesettet tildeles to tall i definisjonssettet, tallet −1 er ikke tilordnet noe nummer på definisjonssettet. - Ofte, i stedet for definisjonssettet, er det i utgangspunktet et kildesett gitt. hvis er gitt som en beregningsregel, oppnår man definisjonssettet ved å ringe fra utelukker de elementene som er ikke definert. Se også avsnittet “ Delfunksjoner ”.
Sett teoretisk definisjon
I settteori er en funksjon en spesiell relasjon :
-
En funksjon av mengden i mengden er mye som har følgende egenskaper: [9]
- er en delmengde av det kartesiske produktet fra og , dvs er et forhold mellom og .
- For hvert element slutten det er minst ett element i slik at det ordnede paret Element i forholdet er. er totalt igjen.
- For hvert element fra det er høyst ett element fra slik at paret i ligger. er derfor juridisk entydig eller funksjonell.
De to siste egenskapene kan også oppsummeres som følger:
-
- For hvert element fra det er nøyaktig ett element fra slik at paret Element i forholdet er.
Ofte vil man imidlertid også eksplisitt gjøre målet satt til en del av funksjonen, for eksempel for å kunne komme med uttalelser om surjektivitet (som en egenskap for funksjonen som er under vurdering):
- Et par består av mye og mange par med en annen mengde kalles settets funksjon til , hvis: For hvert element fra det er nøyaktig ett element fra (skrevet ) slik at paret Element av er.
blir da også grafen til funksjonen kalt. Definisjonen satt funksjonen er unikt bestemt av grafen og består av de første komponentene i alle elementene i grafen. Hvis to funksjoner stemmer overens i grafene, sier den ene også at de i hovedsak er de samme. Spesielt er hver funksjon i hovedsak det samme som den surjektive funksjonen med mengden bilder .
Det er ofte tilrådelig å legge til definisjonssettet og en funksjon som en trippel definere. Denne definisjonen stemmer deretter overens med den tilsvarende detaljerte definisjonen for relasjoner, slik at multifunksjoner og delfunksjoner også registreres på samme måte.
notasjon
Stavemåter
En oppgave kan blant annet beskrives i en av følgende former:
- Funksjonsligning med definisjonssett
- Entydig oppdragsregel (engelsk: maplet ) med definisjonssett
- Tvetydig oppdragsregel med definisjon og målmengde
-
- , eller tilsvarende:
- Familienotasjon (kalt indekssett for definisjonssettet)
- Verditabell (for endelige, men også utallige definisjonssett)
-
1 2 3 4. 5 6. 7. ... 1 4. 9 16 25. 36 49 ...
- Spesielt relasjon representeres også som en delmengde oppregnet eller beskrevet
- Resultat av koblinger og operasjoner (for eksempel sammensetning , dannelse av inversfunksjonen, avledning, etc.) som brukes på andre funksjoner
Måter å snakke på
For tildeling av en funksjonsverdi til et argument Det finnes en rekke forskjellige måter å snakke eller mer detaljert stavemåte på, som alle er mer eller mindre likeverdige og fremfor alt velges avhengig av hva som skal uttrykkes tilsynelatende, av den respektive konteksten, symbolikken som brukes og også av smak av høyttaleren (skribent). Her er noen eksempler:
- er kartlagt fra
- fra vil klart tildelt (spesielt hvis Symbolet er i symbolikken)
- lik fra (spesielt hvis det er et likhetstegn i symbolikken)
- er bildet av under bildet
Dette skal skilles fra måten å snakke og skrive på: " er en funksjon av “, Som fremstår først og fremst på matematikkområder som er svært nært knyttet til fysikk. Det er den eldre og originale måten å snakke og skrive på og beskriver avhengigheten til en variabel fra en annen variabel , i motsetning til det ved hjelp av variabler og (representativ) tildelingen av visse elementer i sett er beskrevet. Den "fysiske" måten å snakke på kommer fra prosedyren, først av alt to variable størrelser (av fysisk virkelighet) symboler, nemlig variablene og , tilordne og deretter bestemme deres avhengighet. For eksempel for romtemperatur og for tiden vil det være mulig å bestemme at romtemperaturen endres som en funksjon av tiden og dermed "romtemperaturen er en funksjon av tiden" eller som en representant " en funksjon av er."
I stedet for et sett med definisjoner sies også å være definisjonsdomene, sett med arketyper eller ganske enkelt arketype . Elementene i kalles funksjonelle argumenter, funksjonelle poeng eller arketyper, tilfeldig også -Verdier. Målbeløpet kalles også et sett med verdier eller et verdiområde , elementene i kalles målverdier eller målelementer , tilfeldig også -Verdier. Disse elementene i som faktisk vises som et bilde av et argument kalles funksjonsverdier, bildeelementer eller ganske enkelt bilder.
fremstilling
En funksjon , kan visualiseres ved å tegne grafen i et (todimensjonalt) koordinatsystem . Funksjonsgrafen til en funksjon kan matematisk defineres som settet til alle elementparene , for er. Grafen til en kontinuerlig funksjon på et tilkoblet intervall danner en tilkoblet kurve (mer presist: settet med punkter på kurven, forstått som et underrom av det topologiske rommet er sammenhengende).
Du kan bruke funksjoner på samme måte , og , visualiser dem ved å tegne dem i et tredimensjonalt koordinatsystem. er kontinuerlig, er resultatet en kurve (som også kan ha hjørner) som "slanger" gjennom koordinatsystemet. er jevnt fremstår et område som et bilde, vanligvis i form av et "fjellandskap".
Dataprogrammer for å representere funksjoner kalles funksjonsplottere . Funksjonsprogrammer er også en del av det funksjonelle omfanget av datamaskinalgebra-systemer (CAS), matrise-kompatible programmeringsmiljøer som MATLAB , Scilab , GNU Octave og andre systemer. De viktigste egenskapene til en funksjonsplotter er også tilgjengelig på en grafisk lommekalkulator . Det finnes også nettbaserte tilbud som bare krever en oppdatert nettleser.
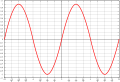
- Eksempler på noen funksjonsgrafer
-
5. grads polynomfunksjon
Grunnleggende egenskaper
Bilde og arketype
Bildet av et element definisjonssettet er ganske enkelt funksjonsverdien . Bildet av en funksjon er settet med bilder av alle elementene i definisjonssettet , så
- .
Bildet av en funksjon er derfor en delmengde av målesettet og kalles bildesettet. Er mer generelt et delsett av , deretter
bildet av under funksjonen .
Arketypen til et element målbeløpet er settet med alle elementene i definisjonssettet hvis bilde er. Det er
- ,
( er generelt ikke en unik funksjon, men en multifunksjon , til notasjon se der, så vel som i relasjon #relasjoner og funksjoner og korrespondanse (matematikk) ).
Ofte er disse fibrene enkle å bruke angir hva, i tilfelle av (unikt) reversible funksjoner, betegner x på den ene siden og { x } på den andre.
Arketypen til et delsett målsett er settet med alle elementene i definisjonssettet hvis bilde er et element i dette delsettet:
- .
Injektivitet, suraktivitet, bijektivitet
- En funksjon er injektiv hvis hvert element i målesettet maksimalt har én arketype. Dvs av følger
- Det er surjektivt hvis hvert element i målsettet har minst én arketype. Det vil si til enhver er det en , så det
- Det er bijektiv når det er injektivt og surjektivt, dvs. når hvert element i målsettet har nøyaktig én arketype.
Arity
En funksjon , definisjonen deres satt en mengde produkt er, betyr ofte to sifre . Verdien av , som ved bruk på paret er oppnådd, skrives (utelater et par parenteser) som
Det samme gjelder høyere arity. En funksjon blir vanligvis referert til som tresifret. En funksjon hvis definisjonssett ikke er et produktsett (eller som definisjonssettets interne struktur ikke spiller noen rolle for) kalles en ensifret funksjon. En nullsifret funksjon er en funksjon hvis definisjonssett er det tomme produktet er, for enhver funksjonsverdi. Derfor kan nullsifrede funksjoner forstås som konstanter , som brukes i algebraiske strukturer (så vel som i heterogene algebraer ).
I stedet for nullsifret, ensifret, tosifret, tresifret sier man også ofte unary, binary, ternary; Arity blir derfor også referert til som "arity".
Sett med funksjoner
med [11] eller blir settet til alle bildene fra til utpekt:
For tykkelsen gjelder følgende:
Operasjoner
Begrensning
Begrensning av en funksjon på et delsett definisjonssettet er funksjonen , hvis graf er av
gitt er.
Invers funksjon
For enhver bijektiv funksjon det er en omvendt funksjon
- ,
så det det unikt bestemte elementet er for det gjelder. Den omvendte funksjonen oppfyller dermed for alle
- .
Bijektive funksjoner blir derfor også referert til som klart reversible funksjoner.
Sammenkobling
To funksjoner og , der verdiområdet for den første funksjonen tilsvarer definisjonsområdet for den andre funksjonen (eller er inneholdt som et delsett), kan lenkes. Kjeden eller sekvensiell utførelse av disse to funksjonene er da en ny funksjon som utføres av
gitt er. I denne notasjonen er den første figuren som vanligvis brukes til høyre, det vil si kl vil fungere først brukt og deretter funksjonen . Av og til brukes imidlertid omvendt rekkefølge i litteraturen og skrevet.
snarvei
Er på målgruppen en indre tosifret lenke gitt, kan den også brukes til funksjoner definere en indre tosifret lenke:
- .
Eksempler på dette er punktvis tillegg og multiplikasjon av funksjoner . Videre, ved hjelp av en ytre tosifret lenke, formen koble også en funksjon til et element definere:
Et eksempel på dette er den punktvise multiplikasjonen av en funksjon med en skalar . En ekstern tilkobling av skjemaet kan være analog definere. Hvis det er lenker av samme type både på definisjonssett og målsett, sies det at en funksjon er kompatibel med disse koblingene hvis bildene oppfører seg på samme måte med hensyn til én lenke som arketypene mht. den andre lenken.
Andre eiendommer
Algebraiske egenskaper
- En funksjon er idempotent hvis er, dvs. for alle elementer definisjonssettet gjelder.
- Hun er imidlertid en involusjon er slik for alle elementer av definisjonssettet gjelder og for minst ett definisjonssettet er.
- Et fast punkt er et element settet med definisjoner av , for gjelder.
- identitet
- Konstans
Analytiske egenskaper
- Tranghet
- periodisitet
- monotoni
- symmetri
- kontinuitet
- Differensiering
- Glatthet
- Holomorfisme
- homogenitet
- Målbarhet
- Integritet
- konveksitet
Spesielle funksjoner
- Real-verdsatt funksjon , som er preget av det faktum at målsettingen ligger innenfor de reelle tallene
- Komplexwertige Funktion , die sich dadurch auszeichnet, dass ihre Zielmenge innerhalb der komplexen Zahlen liegt
- Homogene lineare Funktion (auch: Proportionalität ): allgemein beschrieben durch ; ist ein Homomorphismus bezüglich der Addition
- Allgemeine lineare Funktion (oder affine Funktion ): allg. beschrieben durch ; siehe auch affine Abbildung
- Quadratische Funktion : allg. beschrieben durch (s. Quadratische Gleichung )
- Potenzfunktion
- Polynomfunktionen ; auch ganzrationale Funktion: allg. beschrieben durch oder
- Rationale Funktion ; gebrochen-rationale Funktion: Quotient zweier Polynom-Funktionen,
- Wurzelfunktion : besteht aus gebrochenrationalen Funktionen, verknüpft durch die Grundrechenarten und Wurzelausdrücke
- Exponentialfunktion
- Logarithmus
- Trigonometrische Funktion : sin , cos , tan , cot , sec , csc
- Betragsfunktion
- Maximumsfunktion und Minimumsfunktion
- Gaußsche Ganzzahlfunktion
Verwendung
Ein fundamentales Konzept in der Mathematik stellen Strukturen dar, die dadurch entstehen, dass Mengen in Verbindung mit dazugehörigen Abbildungen gesehen werden. Derartige Strukturen bilden die Grundlage praktisch aller mathematischen Disziplinen, sobald sie über elementare Mengenlehre, kombinatorische Probleme oder grundlegende mathematisch-philosophische Fragestellungen hinausgehen.
Mengen können beispielsweise durch sogenannte Verknüpfungen strukturiert werden. Der wichtigste Spezialfall ist die innere zweistellige Verknüpfung , dabei handelt es sich um eine Abbildung der Form . Beispiele für innere zweistellige Verknüpfungen sind Rechenoperationen, wie die Addition oder Multiplikation auf Zahlenmengen. Dementsprechend wird das Bild eines Paares unter einer Verknüpfung üblicherweise in der Form geschrieben.
Weitere wichtige Beispiele solcher Strukturen sind algebraische , geometrische und topologische Strukturen, wie beispielsweise Skalarprodukte , Normen und Metriken .
Verallgemeinerungen
Multifunktionen
Eine Multifunktion (auch mehrwertige Funktion oder Korrespondenz genannt) ist eine linkstotale Relation. Das heißt, die Elemente der Definitionsmenge können auf mehrere Elemente der Zielmenge abgebildet werden. Man schreibt auch .
Wenn eine Menge ist, dann kann man jede Multifunktion auch als eine Funktion darstellen, die in die Potenzmenge von geht: . [12]
Im Fall stellt eine mehrwertige Funktion eine Transitionsrelation dar, und ist die zugehörige Transitionsfunktion.
Die Verkettung von Multifunktionen lässt sich genauso definieren wie für (eindeutige) Funktionen, mengentheoretisch ist dies äquivalent einer Verkettung zweier zweistelliger Relationen . [13]
Umkehrungen von Funktionen als Multifunktionen
Ein Beispiel für Multifunktionen sind die Umkehrfunktionen (Umkehrungen) von nicht injektiven Funktionen. Wenn surjektiv ist, gilt automatisch: ist eine Multifunktion. Die Darstellung der Umkehrfunktion in die Potenzmenge von liefert mit die Fasern von ( siehe oben ).
Die Verkettung einer Funktion mit ihrer (allgemein nicht eindeutigen) Umkehrung in der Form ist eine Äquivalenzrelation, [14] die durch induzierte Äquivalenzrelation . Zwei Elemente aus dem Definitionsbereich sind genau dann äquivalent, wenn sie denselben Funktionswert haben. [13]
Partielle Funktionen
Wohl zu unterscheiden vom Begriff der Funktion ist der Begriff der partiellen Funktion , man spricht auch von einer „nicht überall definierten Funktion“ oder „ funktionalen Relation “. Hier darf es Elemente der Quellmenge ( -Werte) geben, denen kein Wert der Zielmenge ( -Wert) zugeordnet ist. Hier ist dann die Nennung der Quellmenge in der obigen Tripelschreibweise tatsächlich notwendig. Allerdings darf es auch dort für einen -Wert nicht mehr als einen -Wert geben. Um partielle Funktionen von Funktionen zu unterscheiden, bezeichnet man Letztere auch als totale oder überall definierte Funktionen.
Die Menge [11] der partiellen Abbildungen von nach ist die Vereinigung der totalen Abbildungen von Teilmengen von nach :
Sind die Mengen endlich, so gilt für Ihre Kardinalzahlen
- ,
schließlich kann man jede partielle Abbildung auf D umkehrbar eindeutig zu einer totalen Abbildung fortsetzen, indem man einen beliebigen festen Funktionswert festschreibt, der nicht in enthalten ist; und diese Operation stellt eine bijektive Abbildung auf dar.
Jede partielle Funktion ist im Wesentlichen gleich mit der (totalen) Funktion mit der Urbildmenge .
Funktionen mit Werten in einer echten Klasse
Häufig liegen die Werte einer Funktion nicht in einer Zielmenge, sondern lediglich in einer echten Klasse , beispielsweise sind Mengenfolgen „Funktionen“ mit Definitionsmenge und Werten in der Allklasse . Um die mengentheoretischen Probleme, die sich daraus ergeben, zu vermeiden, betrachtet man nur noch den Graph der entsprechenden Funktion, genauer: Ein funktionsartiger Graph ist eine Menge von Paaren , so dass keine zwei Paare im ersten Eintrag übereinstimmen: [15]
Definitions- und Wertemenge sind tatsächlich Mengen, aber es ist nicht nötig, sich von vornherein auf eine Ziel menge festzulegen, solange die Funktionen im Wesentlichen gleich sind.
Bei partiellen Funktionen gilt gleiches für den Ziel- und Quellbereich. Beide können einzeln oder zusammen echte Klassen sein; mengentheoretische Probleme entstehen nicht, solange der Graph eine Menge bleibt.
Symbolik
Für Funktionen gibt es etliche symbolische Schreibweisen, die jeweils einige spezielle Eigenschaften der Funktion ausdrücken. Im Folgenden werden einige wichtige genannt.
| Symbol | Erklärung |
|---|---|
| Funktion von nach | |
|
|
Funktion, die auf abbildet; statt kann auch ein Term o. Ä. stehen |
|
|
Funktion, die auf abbildet; statt kann auch eine Formel o. Ä. stehen (mengentheoretische Schreibweise) |
| Funktion, die auf abbildet, die die elementweise Zuordnung mit Beschreibung der Funktionssymbolik (statt stehen oft Dinge wie u. Ä.) und der Formel o. Ä. (an der Stelle von ) zur Berechnung des Bildes angibt | |
| Ausführlichste Notation, die alle beteiligten Mengen und die elementweise Zuordnung mit Beschreibung der Funktionssymbolik und der Formel o. Ä. zur Berechnung des Bildes angibt | |
| surjektive Funktion ( Surjektion ) von nach | |
| injektive Funktion ( Injektion ) von nach | |
| bijektive Funktion ( Bijektion ) von nach | |
|
Inklusionsabbildung , natürliche Inklusion, natürliche Einbettung von in ( ist Untermenge von , und die Funktion bildet jedes Element von auf sich ab.) |
|
|
|
Identität, identische Abbildung auf A oder von nach ( und die Funktion bildet jedes Element auf sich ab.) |
|
|
Isomorphismus von nach |
|
|
partielle Funktion (so) von nach |
| mehrwertige Funktion, Multifunktion , Korrespondenz (so) von nach | |
|
(bzw. …) |
Menge der Funktionen (bzw. partiellen Funktionen), … von nach [11] |
Die Symbole können auch, wo sinnvoll, miteinander kombiniert werden.
Literatur
- Heinz-Dieter Ebbinghaus : Einführung in die Mengenlehre. 4. Auflage. Spektrum, Akademischer Verlag, Heidelberg ua 2003, ISBN 3-8274-1411-3 .
- Paul R. Halmos : Naive Mengenlehre (= Moderne Mathematik in elementarer Darstellung. Bd. 6). Übersetzt von Manfred Armbrust und Fritz Ostermann. 5. Auflage. Vandenhoeck & Ruprecht, Göttingen 1994, ISBN 3-525-40527-8 .
- Arnold Oberschelp : Allgemeine Mengenlehre. BI-Wissenschafts-Verlag, Mannheim ua 1994, ISBN 3-411-17271-1 .
- Adolf P. Youschkevitch: The Concept of Function up to the Middle of the 19th Century. In: Archive of the History of Exakt Sciences. 16 Springer Verlag, Berlin 1976.
Weblinks
Einzelnachweise und Anmerkungen
- ↑ M. Kronfellner: Historische Aspekte im Mathematikunterricht. Verlag Hölder-Pichler-Tempsky, Wien 1998, S. 67.
- ↑ Adolf P. Youschkevitch: The Concept of Function up to the Middle of the 19th Century. In: Archive of the History of Exakt Sciences. 16, Springer Verlag, Berlin 1976, S. 52.
- ↑ D. Rüthing: Einige historische Stationen zum Funktionsbegriff. In: Der Mathematikunterricht. Heft 6/1986, Friedrich Verlag Velber, S. 5–6.
- ↑ H.-J. Vollrath: Algebra in der Sekundarstufe. BI Wissenschaftsverlag, Mannheim 1994, S. 118.
- ↑ Rüthing, S. 6–12.
- ↑ Arnold Oberschelp: Allgemeine Mengenlehre. 1994.
- ↑ Klassenfunktion genannt, siehe Claudius Röhl: Das Auswahlaxiom , Diplomarbeit Univ. Leipzig, Fakultät für Mathematik, 6. Oktober 2016, Seite 18
-
↑ Funktionen, deren Zielmengen sich nur in diesen (wertlosen) Nichtbild-Elementen unterscheiden, werden gelegentlich als gleich angesehen, insbesondere dann, wenn keine von ihnen surjektiv ist. Also:
- ↑ Paul R. Halmos: Naive Mengenlehre . 1994, Kapitel 8, S. 43 .
- ↑ seltener in Anlehnung an die Mengenschreibweise äquivalent
- ↑ a b c teilweise auch ohne die eckigen Klammern notiert
-
↑ beziehungsweise entsprechend der vereinfachten Funktionsdefinition mit Funktion=Graph. Alternative Bezeichnungsweisen:
- oder für die Korrespondenz zur Multifunktion , im Fall ( Transitionsfunktion ) auch
- oder für die Potenzmenge von
- ↑ a b H. König: Entwurf und Strukturtheorie von Steuerungen für Fertigungseinrichtungen (= ISW Forschung und Praxis . Band 13 ). Springer-Verlag, Berlin / Heidelberg 1976, ISBN 3-540-07669-7 , S. 15–17 , doi : 10.1007/978-3-642-81027-5_1 . Hier: Seite 21f
- ↑ wie immer für zweistellige Relationen; wir fassen die Funktion als zweistellige Relation auf, erst recht ihre Umkehrung
- ↑ Nicolas Bourbaki : Éléments de mathématiques. Théorie des Ensembles. II.
- ↑ Die Notation wird von manchmal abweichend für (beliebige) Relationen gebraucht.
- Mathematische Funktion
- Mengenlehre
- Mathematischer Grundbegriff
































































![{\ displaystyle Z ^ {D}, \ {} ^ {D} Z, \ [D \ til Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8a3efbec5b42fa81ba2142e9a623bc670681851)





















































![{\displaystyle [D\rightharpoonup Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad0c804a555ba1b55160981ae0e4384eaa84c3c1)
![{\displaystyle [D\rightharpoonup Z]=\bigcup \limits _{X\subseteq {D}}[X\to Z]=\bigcup \limits _{X\subseteq {D}}Z^{X}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49acf8342679017f23cf89d4e5e218788a8d7154)
![{\displaystyle \left|[D\rightharpoonup Z]\right|=(|Z|+1)^{|D|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e63327c2efce22d696c88445af6e9d7183f615c0)































![{\displaystyle [A\to B]=B^{A}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd84487e3ecce4319bfbc282ef2adb22713f616a)
![{\displaystyle [A\rightharpoonup B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cf08908d7847e96631a3b47862b405584be38fb)









