Desimal system

En desimal system (fra Middle latin decimalis, til latin desem "ti"), også kjent som desimalsystemet eller desimalsystemet, er et tallsystem som bruker tallet 10 som basen .

Som regel forstås det spesifikt å bety desimalsystemet med stedverdisystem , som ble utviklet med indiske tall , videreført til europeiske land gjennom arabisk mekling og nå er etablert over hele verden som en internasjonal standard.

Imidlertid er desimalsystemer også tallsystemer basert på 10 uten et stedverdisystem , ettersom de er basert på tallene til mange naturlige språk og eldre tall , noen ganger i forbindelse med quinære , vigesimale eller andre tallsystemer.

Antropologisk er fremveksten av desimalsystemer - og kinesiske systemer - knyttet til menneskers to ganger fem fingre . Disse tjente som telling og aritmetiske hjelpemidler ( finger aritmetisk ). Denne forklaringen støttes av tall for 5 ("hånd") og 10 ("to hender") på flere språk. ^[1]

Verdisystem for desimaler

Siffer

Ti sifre brukes i desimalsystemet

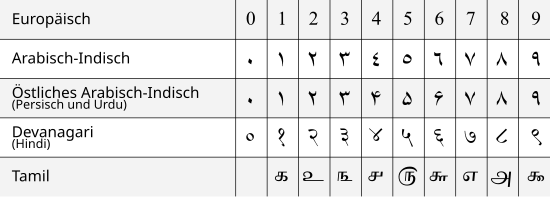
0 (null) , 1 (en) , 2 (to) , 3 (tre) , 4 (fire) , 5 (fem) , 6 (seks) , 7 (syv) , 8 (åtte) , 9 (ni) ,

referert til som desimal siffer .

Imidlertid er disse sifrene stavet annerledes i forskjellige deler av verden.

Indiske tall brukes fremdeles i dag i de forskjellige indiske skriptene ( Devanagari , bengalsk skrift , tamilsk skrift , etc.). De er veldig forskjellige fra hverandre.

definisjon

I den tysktalende verden er det vanligvis et desimaltall i formen

z_{m}\,z_{m-1}\,\ldots \,z_{0}\,\operatorname {,} \,z_{-1}\,z_{-2}\,\ldots \,z_{-n}\qquad \left(m,n\in \mathbb {N} \quad z_{i}\in \{0,\ldots ,9\}\right)

{\ displaystyle z_ {m} \, z_ {m-1} \, \ ldots \, z_ {0} \, \ operatorname {,} \, z _ {- 1} \, z _ {- 2} \, \ ldots \, z _ {- n} \ qquad \ left (m, n \ in \ mathbb {N} \ quad z_ {i} \ in \ {0, \ ldots, 9 \} \ right)}

{\ displaystyle z_ {m} \, z_ {m-1} \, \ ldots \, z_ {0} \, \ operatorname {,} \, z _ {- 1} \, z _ {- 2} \, \ ldots \, z _ {- n} \ qquad \ left (m, n \ in \ mathbb {N} \ quad z_ {i} \ in \ {0, \ ldots, 9 \} \ right)}

skrevet ned; I tillegg er det andre skrivemåter avhengig av formål og plassering. Alle er der $z_{i}$ ${\ displaystyle z_ {i}}$ $z_ {i}$ en av sifrene ovenfor. Hvert siffer har en numerisk verdi og, avhengig av posisjonen, en stedsverdi. Den numeriske verdien er i konvensjonell tellerekkefølge. Indeksen $Jeg$ ${\ displaystyle i}$ $Jeg$ bestemmer verdien, dette er kraften til ti $10^{i}$ ${\ displaystyle 10 ^ {i}}$ ${\ displaystyle 10 ^ {i}}$ . Sifrene skrives etter hverandre uten skilletegn, hvorved det mest betydningsfulle sifferet begynner med sifferet $z_{m}$ ${\ displaystyle z_ {m}}$ $z_ {m}$ helt til venstre og de nederste sifrene med sifrene $z_{m-1}$ ${\ displaystyle z_ {m-1}}$ $z _ {{m-1}}$ før $z_{0}$ ${\ displaystyle z_ {0}}$ $z_ {0}$ er til høyre for det i synkende rekkefølge. For å representere rasjonelle tall med ikke-periodisk utvikling, følger sifrene etter et skilletegn $z_{-1}$ ${\ displaystyle z _ {- 1}}$ $z _ {{- 1}}$ før $z_{-n}$ ${\ displaystyle z _ {- n}}$ $z _ {{- n}}$ . I den engelsktalende verden brukes et punkt i stedet for komma.

Verdien $Z$ ${\ displaystyle Z}$ $Z$ desimaltallet oppnås dermed ved å legge opp disse sifrene, som deretter multipliseres med deres plassverdi; i tillegg skal skiltet settes foran; et tegn som mangler betyr et pluss:

Z=\sum _{i=-n}^{m}z_{i}\cdot 10^{i}\geq 0\ ;\qquad Z=-\sum _{i=-n}^{m}z_{i}\cdot 10^{i}\leq 0

{\ displaystyle Z = \ sum _ {i = -n} ^ {m} z_ {i} \ cdot 10 ^ {i} \ geq 0 \; \ qquad Z = -\ sum _ {i = -n} ^ { m} z_ {i} \ cdot 10 ^ {i} \ leq 0}

{\ displaystyle Z = \ sum _ {i = -n} ^ {m} z_ {i} \ cdot 10 ^ {i} \ geq 0 \; \ qquad Z = -\ sum _ {i = -n} ^ { m} z_ {i} \ cdot 10 ^ {i} \ leq 0}

.

Denne representasjonen kalles også desimal brøk utvikling .

Eksempel:

7023{,}48=7\cdot 10^{3}+0\cdot 10^{2}+2\cdot 10^{1}+3\cdot 10^{0}+4\cdot 10^{-1}+8\cdot 10^{-2}

{\ displaystyle 7023 {,} 48 = 7 \ ganger 10 ^ {3} +0 \ ganger 10 ^ {2} +2 \ ganger 10 ^ {1} +3 \ ganger 10 ^ {0} +4 \ ganger 10 ^ {-1} +8 \ cdot 10 ^ {- 2}}

{\ displaystyle 7023 {,} 48 = 7 \ ganger 10 ^ {3} +0 \ ganger 10 ^ {2} +2 \ ganger 10 ^ {1} +3 \ ganger 10 ^ {0} +4 \ ganger 10 ^ {-1} +8 \ cdot 10 ^ {- 2}}

Med oppløste potens får vi:

7023{,}48=7\cdot 1000+0\cdot 100+2\cdot 10+3\cdot 1+4\cdot 0{,}1+8\cdot 0{,}01

{\ displaystyle 7023 {,} 48 = 7 \ cdot 1000 + 0 \ cdot 100 + 2 \ cdot 10 + 3 \ cdot 1 + 4 \ cdot 0 {,} 1 + 8 \ cdot 0 {,} 01}

{\ displaystyle 7023 {,} 48 = 7 \ cdot 1000 + 0 \ cdot 100 + 2 \ cdot 10 + 3 \ cdot 1 + 4 \ cdot 0 {,} 1 + 8 \ cdot 0 {,} 01}

Utvikling av desimalbrøk (konvertering av periodiske desimaltall til brøk)

Ved hjelp av utvidelsen av desimalbrøk kan du tilordne en sifferrekke til hvert reelt tall . Hver begrensede del av denne sekvensen definerer en desimalbrøk , som er en tilnærming til det reelle tallet. Selve det reelle tallet oppnås ved å flytte fra endelige summer av delene til den uendelige serien over alle sifre.

Formell blir med $z=0,a_{1}a_{2}a_{3}\ldots$ ${\ displaystyle z = 0, a_ {1} a_ {2} a_ {3} \ ldots}$ $z = 0, a_ {1} a_ {2} a_ {3} \ ldots$ så verdien av serien $\textstyle \sum _{i=1}^{\infty }a_{i}10^{-i}$ ${\ displaystyle \ textstyle \ sum _ {i = 1} ^ {\ infty} a_ {i} 10 ^ {- i}}$ $\ textstyle \ sum _ {{i = 1}} ^ {{\ infty}} a_ {i} 10 ^ {{- i}}$ utpekt.

Det sies at desimalbrøkutviklingen stopper når siffresekvensen fra en posisjon n består av bare nuller, dvs. det virkelige tallet som vises er allerede en desimalbrøk i seg selv. Spesielt med alle irrasjonelle tall , brytes ikke sifresekvensen; det er en uendelig desimal brøkekspansjon.

Følgende forhold brukes til å transformere periodisk utvidelse av desimalbrøk :

0{,}{\overline {1}}={\frac {1}{9}};\quad 0{,}{\overline {01}}={\frac {1}{99}};\quad 0{,}{\overline {001}}={\frac {1}{999}};\quad \ldots

{\ displaystyle 0 {,} {\ overline {1}} = {\ frac {1} {9}}; \ quad 0 {,} {\ overline {01}} = {\ frac {1} {99}} ; \ quad 0 {,} {\ overline {001}} = {\ frac {1} {999}}; \ quad \ ldots}

0 {,} \ overline {1} = {\ frac {1} {9}}; \ quad 0 {,} \ overline {01} = {\ frac {1} {99}}; \ quad 0 {,} \ overline {001} = {\ frac {1} {999}}; \ quad \ ldots

.

Disse identitetene stammer fra beregningsreglene for geometriske serier , ifølge hvilke $\textstyle \sum _{i=0}^{\infty }q^{i}={\frac {1}{1-q}}$ ${\ displaystyle \ textstyle \ sum _ {i = 0} ^ {\ infty} q ^ {i} = {\ frac {1} {1-q}}}$ $\ textstyle \ sum _ {{i = 0}} ^ {{\ infty}} q ^ {{i}} = {\ frac {1} {1-q}}$ til $q<1$ ${\ displaystyle q <1}$ $q <1$ gjelder. I det første eksemplet du velger $q=10^{-1}$ ${\ displaystyle q = 10 ^ {- 1}}$ $q = 10 ^ {{- 1}}$ og summeringen begynner bare med det første uttrykket i sekvensen.

Eksempler:

0{,}55555\ldots =0{,}{\overline {5}}={\frac {5}{9}}

{\ displaystyle 0 {,} 55555 \ ldots = 0 {,} {\ overline {5}} = {\ frac {5} {9}}}

0 {,} 55555 \ ldots = 0 {,} \ overline {5} = {\ frac {5} {9}}

0{,}33333\ldots =0{,}{\overline {3}}={\frac {3}{9}}={\frac {1}{3}}

{\ displaystyle 0 {,} 33333 \ ldots = 0 {,} {\ overline {3}} = {\ frac {3} {9}} = {\ frac {1} {3}}}

0 {,} 33333 \ ldots = 0 {,} \ overline {3} = {\ frac {3} {9}} = {\ frac {1} {3}}

0{,}424242\ldots =0{,}{\overline {42}}={\frac {42}{99}}={\frac {14}{33}}

{\ displaystyle 0 {,} 424242 \ ldots = 0 {,} {\ overline {42}} = {\ frac {42} {99}} = {\ frac {14} {33}}}

0 {,} 424242 \ ldots = 0 {,} \ overline {42} = {\ frac {42} {99}} = {\ frac {14} {33}}

0{,}081081081\ldots =0{,}{\overline {081}}={\frac {81}{999}}={\frac {3}{37}}

{\ displaystyle 0 {,} 081081081 \ ldots = 0 {,} {\ overline {081}} = {\ frac {81} {999}} = {\ frac {3} {37}}}

0 {,} 081081081 \ ldots = 0 {,} \ overline {081} = {\ frac {81} {999}} = {\ frac {3} {37}}

Perioden overføres til disken i hvert enkelt tilfelle. Det er like mange ni i nevneren som det er sifre i perioden. Om nødvendig bør den resulterende pausen forkortes .

Beregningen er litt mer komplisert hvis perioden ikke umiddelbart følger desimaltegnet:

Eksempler:

0{,}83333\ldots =0{,}8{\overline {3}}=8{,}{\overline {3}}:10=\left(8+{\frac {3}{9}}\right):10=\left(8+{\frac {1}{3}}\right):10={\frac {25}{3}}:10={\frac {25}{30}}={\frac {5}{6}}

{\ displaystyle 0 {,} 83333 \ ldots = 0 {,} 8 {\ overline {3}} = 8 {,} {\ overline {3}}: 10 = \ left (8 + {\ frac {3} { 9}} \ høyre): 10 = \ venstre (8 + {\ frac {1} {3}} \ høyre): 10 = {\ frac {25} {3}}: 10 = {\ frac {25} { 30}} = {\ frac {5} {6}}}

{\ displaystyle 0 {,} 83333 \ ldots = 0 {,} 8 {\ overline {3}} = 8 {,} {\ overline {3}}: 10 = \ left (8 + {\ frac {3} { 9}} \ høyre): 10 = \ venstre (8 + {\ frac {1} {3}} \ høyre): 10 = {\ frac {25} {3}}: 10 = {\ frac {25} { 30}} = {\ frac {5} {6}}}

0{,}492363636\ldots =0{,}492{\overline {36}}=492{,}{\overline {36}}:1000=492{\frac {36}{99}}:1000=492{\frac {4}{11}}:1000={\frac {5416}{11}}:1000={\frac {5416}{11000}}={\frac {677}{1375}}

{\ displaystyle 0 {,} 492363636 \ ldots = 0 {,} 492 {\ overline {36}} = 492 {,} {\ overline {36}}: 1000 = 492 {\ frac {36} {99}}: 1000 = 492 {\ frac {4} {11}}: 1000 = {\ frac {5416} {11}}: 1000 = {\ frac {5416} {11000}} = {\ frac {677} {1375}} }

0 {,} 492363636 \ ldots = 0 {,} 492 \ overline {36} = 492 {,} \ overline {36}: 1000 = 492 {\ frac {36} {99}}: 1000 = 492 {\ frac { 4} {11}}: 1000 = {\ frac {5416} {11}}: 1000 = {\ frac {5416} {11000}} = {\ frac {677} {1375}}

13{,}54323232\ldots =13{,}54{\overline {32}}

{\ displaystyle 13 {,} 54323232 \ ldots = 13 {,} 54 {\ overline {32}}}

13 {,} 54323232 \ ldots = 13 {,} 54 \ overline {32}

Første trinn: Du multipliserer startnummeret med en potens på ti slik at nøyaktig en periode (i eksempel 32) er foran desimaltegnet:

x=13{,}543232\ldots |\cdot 10{.}000

{\ displaystyle x = 13 {,} 543232 \ ldots | \ cdot 10 {.} 000}

x = 13 {,} 543232 \ ldots | \ cdot 10 {.} 000

10{.}000\cdot x=135{.}432{,}3232\ldots

{\ displaystyle 10 {.} 000 \ cdot x = 135 {.} 432 {,} 3232 \ ldots}

10 {.} 000 \ cdot x = 135 {.} 432 {,} 3232 \ ldots

Trinn 2: så multipliserer du startnummeret med en potens på ti slik at periodene begynner nøyaktig etter desimaltegnet:

x=13{,}543232\ldots |\cdot 100

{\ displaystyle x = 13 {,} 543232 \ ldots | \ cdot 100}

x = 13 {,} 543232 \ ldots | \ cdot 100

100\cdot x=1{.}354{,}323232\ldots

{\ displaystyle 100 \ cdot x = 1 {.} 354 {,} 323232 \ ldots}

100 \ cdot x = 1 {.} 354 {,} 323232 \ ldots

3. trinn: trekk fra de to linjene som ble opprettet ved trinn 1 og 2 fra hverandre: (punktumene etter desimaltegnet er utelatt)

10{.}000\cdot x=135{.}432{,}323232\ldots

{\ displaystyle 10 {.} 000 \ cdot x = 135 {.} 432 {,} 323232 \ ldots}

10 {.} 000 \ cdot x = 135 {.} 432 {,} 323232 \ ldots

(Linje 1)

100\cdot x=1354{,}323232\ldots

{\ displaystyle 100 \ cdot x = 1354 {,} 323232 \ ldots}

100 \ cdot x = 1354 {,} 323232 \ ldots

(Linje 2)

9{.}900\cdot x=135{.}432-1{.}354=134{.}078\!

{\ displaystyle 9 {.} 900 \ cdot x = 135 {.} 432-1 {.} 354 = 134 {.} 078 \!}

9 {.} 900 \ cdot x = 135 {.} 432-1 {.} 354 = 134 {.} 078 \!

(Rad 1 minus rad 2)

Fjerde trinn: bytte

9{.}900\cdot x=134{.}078|:9{.}900

{\ displaystyle 9 {.} 900 \ cdot x = 134 {.} 078 |: 9 {.} 900}

9 {.} 900 \ cdot x = 134 {.} 078 |: 9 {.} 900

Resultat:

x={\frac {134{.}078}{9{.}900}}=13{,}54{\overline {32}}

{\ displaystyle x = {\ frac {134 {.} 078} {9 {.} 900}} = 13 {,} 54 {\ overline {32}}}

x = {\ frac {134 {.} 078} {9 {.} 900}} = 13 {,} 54 \ overline {32}

Uklarhet i representasjon

Et særtrekk ved utvidelsen av desimal brøk er at mange rasjonelle tall har to forskjellige desimal brøk utvidelser. Som beskrevet ovenfor kan du $0{,}{\overline {9}}$ ${\ displaystyle 0 {,} {\ overline {9}}}$ $0 {,} \ overline {9}$ omforme og til uttalelsen

0{,}{\overline {9}}={\frac {9}{9}}=1

{\ displaystyle 0 {,} {\ overline {9}} = {\ frac {9} {9}} = 1}

0 {,} \ overline {9} = {\ frac {9} {9}} = 1

nå, se artikkel 0.999 ...

Fra denne identiteten kan man videre utlede at mange rasjonelle tall (nemlig alle med endelig desimal brøkvidde med unntak av 0) kan representeres på to forskjellige måter: enten som en endelig desimal brøk med punkt 0, eller som uendelig desimal brøk med punktum 9. For å gjøre representasjonen entydig For å gjøre dette kan du ganske enkelt forby periode 9 (eller sjeldnere periode 0).

formel

Følgende formel kan settes opp for periodiske desimalbrøk med null foran desimaltegnet:

p={\frac {x\cdot \left(10^{n}-1\right)+y}{10^{m}\cdot \left(10^{n}-1\right)}}

{\ displaystyle p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)} }}

p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)}}

Her er p tallet, x er tallet før begynnelsen av perioden (som et heltall), m er antall siffer før begynnelsen av perioden, y er sekvensen av siffer i perioden (som et heltall) og n er lengden på perioden.

Anvendelsen av denne formelen bør demonstreres ved å bruke det siste eksemplet:

p=0{,}492363636\ldots =0{,}492{\overline {36}}

{\ displaystyle p = 0 {,} 492363636 \ ldots = 0 {,} 492 {\ overline {36}}}

p = 0 {,} 492363636 \ ldots = 0 {,} 492 \ overline {36}

x=492;\quad m=3;\quad y=36;\quad n=2

{\ displaystyle x = 492; \ quad m = 3; \ quad y = 36; \ quad n = 2}

x = 492; \ quad m = 3; \ quad y = 36; \ quad n = 2

p={\frac {x\cdot \left(10^{n}-1\right)+y}{10^{m}\cdot \left(10^{n}-1\right)}}={\frac {492\cdot \left(10^{2}-1\right)+36}{10^{3}\cdot \left(10^{2}-1\right)}}={\frac {492\cdot 99+36}{1000\cdot 99}}={\frac {48744}{99000}}={\frac {677}{1375}}

{\ displaystyle p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)} } = {\ frac {492 \ cdot \ left (10 ^ {2} -1 \ right) +36} {10 ^ {3} \ cdot \ left (10 ^ {2} -1 \ right)}} = { \ frac {492 \ cdot 99 + 36} {1000 \ cdot 99}} = {\ frac {48744} {99000}} = {\ frac {677} {1375}}}

p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)}} = { \ frac {492 \ cdot \ left (10 ^ {2} -1 \ right) +36} {10 ^ {3} \ cdot \ left (10 ^ {2} -1 \ right)}} = {\ frac { 492 \ cdot 99 + 36} {1000 \ cdot 99}} = {\ frac {48744} {99000}} = {\ frac {677} {1375}}

periode

I matematikk er perioden med en desimalbrøk et siffer eller en sekvens av sifre som gjentas igjen og igjen etter desimaltegnet. Alle rasjonelle tall , og bare disse, har en periodisk utvidelse av desimalbrøk.

Eksempler:

Rent periodisk: (perioden begynner umiddelbart etter desimaltegnet)

1/3 = 0, ... 3 3333

1/7 = 0, 142857 142857 ...

1/9 = 0, 1 1111 ...

Blandet periodisk: (etter desimalpunktet er det en tidligere periode før perioden begynner)

2/55 = 0,0 36 363636 ... (forrige periode 0; periode lengde 2)

1/30 = 0,0 3 333 ... (forrige periode 0; periode lengde 1)

1/6 = 0,1 6 666 ... (forrige periode 1; periode lengde 1)

134078/9900 = 13,54 32 32 ... (forrige periode er 54; periodelengde er 2)

Endelige desimalfraksjoner teller også blant de periodiske desimalbrøkene; etter å ha satt inn et uendelig antall nuller, for eksempel 0,12 = 0,12000 ...

Ekte perioder (dvs. ingen endelige desimalfraksjoner) forekommer i desimalsystemet nøyaktig når nevneren til den underliggende brøken ikke kan genereres utelukkende av primfaktorene 2 og 5. 2 og 5 er hovedfaktorene til tallet 10, grunnlaget for desimalsystemet. Er nevneren et primtall $s$ ${\ displaystyle p}$ $s$ (bortsett fra 2 og 5), har perioden en maksimal lengde som er en mindre enn verdien til nevneren (vist med fet skrift i eksemplene).

Periodenes eksakte lengde fra $1/p$ ${\ displaystyle 1 / p}$ $1 / s$ (hvis primtallet verken er 2 eller 5) tilsvarer det minste naturlige tallet $n$ ${\ displaystyle n}$ $n$ , i $s$ ${\ displaystyle p}$ $s$ i hovedfaktoriseringen av $R_{n}={10^{n}-1}$ ${\ displaystyle R_ {n} = {10 ^ {n} -1}}$ $R_ {n} = {10 ^ {n} -1}$ inntreffer.

Eksempel på periodelengde 6 : (10 ⁶ - 1) = 999,999:

999,999 = 3 x 3 x 3 x 7 · 11 · 13 · 37 1/7 = 0, ... 142857 142857 og 1/13 = 0, 076 923 076 923 ...

Både 1/7 og 1/13 har en periodelengde på 6 fordi 7 og 13 vises for første gang i primfaktoriseringen på 10 ⁶ - 1. Imidlertid har 1/37 en periode på bare 3, fordi allerede (10 ³ - 1) = 999 = 3 · 3 · 3 · 37.

Hvis nevneren ikke er et primtall, blir periodelengden tilsvarende tallet $n$ ${\ displaystyle n}$ $n$ , der nevneren er første gang en deler av $R_{n}={10^{n}-1}$ ${\ displaystyle R_ {n} = {10 ^ {n} -1}}$ $R_ {n} = {10 ^ {n} -1}$ er; hovedfaktorene 2 og 5 i nevneren er ikke tatt i betraktning.

Eksempler: 1/185 = 1/(5 * 37) har samme periodelengde som 1/37, nemlig 3.

1/143 = 1 / (11 13) har periodelengden 6, fordi 999,999 = 3 3 3 7 143 37 (se ovenfor)

1/260 = 1/(2 · 2 · 5 · 13) har samme periodelengde som 1/13, dvs. 6.

Om perioden lengde $n$ ${\ displaystyle n}$ $n$ For effektivt å bestemme primfaktoriseringen av den raskt voksende sekvensen med tall 9, 99, 999, 9999 etc. kan unngås ved å bruke det tilsvarende forholdet $10^{n}\equiv 1{\pmod {k}}$ ${\ displaystyle 10 ^ {n} \ equiv 1 {\ pmod {k}}}$ $10 ^ {n} \ equiv 1 {\ pmod k}$ brukes, dvs. gjentatt multiplikasjon (starter med 1) med 10 modulo av den nevnte nevneren $k$ ${\ displaystyle k}$ $k$ til dette er lik 1 igjen. For eksempel for $k=13$ ${\ displaystyle k = 13}$ $k = 13$ :

10^{1}\equiv 10{\pmod {13}}

{\ displaystyle 10 ^ {1} \ equiv 10 {\ pmod {13}}}

10 ^ {1} \ equiv 10 {\ pmod {13}}

,

10^{2}\equiv 10\cdot 10\equiv 100\equiv 9{\pmod {13}}

{\ displaystyle 10 ^ {2} \ equiv 10 \ cdot 10 \ equiv 100 \ equiv 9 {\ pmod {13}}}

10 ^ {2} \ equiv 10 \ cdot 10 \ equiv 100 \ equiv 9 {\ pmod {13}}

,

10^{3}\equiv 9\cdot 10\equiv 90\equiv 12{\pmod {13}}

{\ displaystyle 10 ^ {3} \ equiv 9 \ cdot 10 \ equiv 90 \ equiv 12 {\ pmod {13}}}

10 ^ {3} \ equiv 9 \ cdot 10 \ equiv 90 \ equiv 12 {\ pmod {13}}

,

10^{4}\equiv 12\cdot 10\equiv 120\equiv 3{\pmod {13}}

{\ displaystyle 10 ^ {4} \ equiv 12 \ cdot 10 \ equiv 120 \ equiv 3 {\ pmod {13}}}

10 ^ {4} \ equiv 12 \ cdot 10 \ equiv 120 \ equiv 3 {\ pmod {13}}

,

10^{5}\equiv 3\cdot 10\equiv 30\equiv 4{\pmod {13}}

{\ displaystyle 10 ^ {5} \ equiv 3 \ cdot 10 \ equiv 30 \ equiv 4 {\ pmod {13}}}

10 ^ {5} \ equiv 3 \ cdot 10 \ equiv 30 \ equiv 4 {\ pmod {13}}

,

10^{6}\equiv 4\cdot 10\equiv 40\equiv 1{\pmod {13}}

{\ displaystyle 10 ^ {6} \ equiv 4 \ cdot 10 \ equiv 40 \ equiv 1 {\ pmod {13}}}

10 ^ {6} \ equiv 4 \ cdot 10 \ equiv 40 \ equiv 1 {\ pmod {13}}

,

så 1/13 har periodelengden 6. ^[2]

notasjon

For periodiske desimalbrøk er en notasjon vanlig der den periodisk gjentatte delen av desimalene er markert med en overlinje . eksempler er

$1/6=0{,}1{\bar {6}}$ ${\ displaystyle 1/6 = 0 {,} 1 {\ bar {6}}}$ $1/6 = 0 {,} 1 {\ bar {6}}$ ,
$1/7=0{,}{\overline {142857}}$ ${\ displaystyle 1/7 = 0 {,} {\ overline {142857}}}$ $1/7 = 0 {,} \ overline {142857}$ .

På grunn av tekniske begrensninger eksisterer også andre konvensjoner. Overlinjen kan plasseres foran, typografisk vekt (fet, kursiv, understreket) for den periodiske delen kan velges, eller den kan settes i parentes:

1/6 = 0,1¯6 = 0,1 6 = 0,1 6 = 0,1 6 = 0,1 (6)
1/7 = 0, ¯142857 = 0, 142857 = 0, 142857 = 0, 142857 = 0, (142857)

Ikke-periodisk sekvens av sifre etter desimaltegnet

Som forklart i artikkelen stedverdisystem , har irrasjonelle tall (også) i desimalsystemet en uendelig, ikke-periodisk sekvens av sifre etter desimaltegnet. Irrasjonelle tall kan ikke representeres av en endelig eller en periodisk sekvens av sifre. Man kan nærme seg med endelige (eller periodiske) desimalbrøk etter ønske, men en slik begrenset representasjon er aldri eksakt. Så det er bare mulig ved hjelp av flere symboler å indikere irrasjonelle tall gjennom begrensede representasjoner.

Eksempler på slike symboler er rottegn , for eksempel for ${\sqrt {2}}$ ${\ displaystyle {\ sqrt {2}}}$ ${\ sqrt {2}}$ , Bokstaver som π eller e , samt matematiske uttrykk som uendelige serier eller grenseverdier .

Konvertering til andre stedsverdisystemer

Metoder for å konvertere fra og til desimalsystemet er beskrevet i artiklene om andre stedsverdisystemer og under tallbaseendring og stedsverdisystem .

historie

Et av de eldste bevisene på desimal vorschriftlicher -kulturer som ble funnet i en skare av Oberding fra tidlig bronsealder (rundt 1650 v. Chr.) Med 791 stort sett standardiserte låsestenger av kobber fra Salzburg og Slovakia. Flertallet av disse stolpene hadde blitt plassert i grupper på 10 x 10 bunter. ^[3] ^[4]

Desimalsystemer - fremdeles uten et stedverdisystem og uten representasjon av nullene - var grunnlaget for tallskriftene til blant annet egypterne , minoerne , grekerne og romerne . Disse var additiv tall fonter, med hvilke tall kan skrives ned som et minne hjelpemiddel når beregning , men aritmetiske operasjoner kan egentlig ikke bli utført skriftlig: disse var heller med mental aritmetikk eller sammen med andre hjelpemidler som for eksempel beregning av steiner (gresk psephoi, Latin calculi , i slutten av middelalderen også kalt aritmetic pennies or French chips ) på aritmetikken på linjer og muligens med fingertallene .

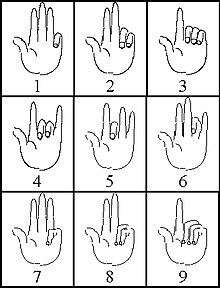
Fingretall ifølge Beda Venerabilis , venstre hånd

Fingretall ifølge Beda Venerabilis, venstre hånd

Fingertallene, som var utbredt i romersk og middelalder og også ble brukt i en litt annen form i den arabiske verden, var basert på et desimalsystem for representasjonen av tallene 1 til 9999, uten et symbol for null, og med et posisjonssystem for sine egne fingerposisjoner på venstre hånd med liten, ring og langfinger enhetene 1 til 9 og med pekefingeren og tommelen tiere til 90, mens på høyre hånd hundrevis med tommel og pekefinger er en speilbilde av titalls og tusenvis med de tre gjenværende fingrene ble vist som et speilbilde av de. ^[5] Disse fingertallene sies å ha blitt brukt ikke bare for å telle og huske tall, men også for regning; De samtidige skriftlige kildene er imidlertid begrenset til beskrivelsen av fingerposisjonene og gir ikke mer detaljert informasjon om de matematiske operasjonene som kan utføres med dem.

Roman handabacus (rekonstruksjon)

På abakusen i den gresk-romerske antikken og den kristne middelalderen, på den annen side, var et fullverdig desimalverdisystem tilgjengelig for representasjon av hele tall, ved at for et gitt tall var antallet av dem, tiere, hundrevis osv. ble representert ved å beregne steiner i tilsvarende vertikale desimalkolonner. På den gamle abacus ble dette gjort ved å plassere eller skyve et tilsvarende antall beregninger i den respektive desimalkolonnen, hvorved en samling på fem også ble praktisert, med fem enheter hver representert med en enkelt beregning i et spesialområde på siden eller øverst i desimalkolonnen. ^[6] I klosteret Abacus i tidlig middelalder, nå for det meste kalt Gerbert er koblet til det 12. århundre var i bruk fra det 10., var i stedet antall enheter i den respektive desimalkolonnen representert bare av en enkelt stein, med en Antall ble nummerert fra 1 til 9, ^[7] mens senere middelalder og tidlig moderne tid vendte tilbake til bruk av ikke -nummererte aritmetiske steiner og kolonnene eller nå horisontalt tegnet linjer enten for desimalregning med hele tall ved grunnnummer 10 (med fem bunter), ^[8] eller for økonomisk regnskap basert på de monetære grunnenhetene som er arvet fra den karolingiske mynten (1 libra = 20 solidi = 240 denarii) ikke-desimalt. ^[9] På de eldgamle og middelalderske versjonene av denne hjelpen ble verdien null vist ved å la den relevante desimalkolonnen eller linjen stå tom, og så også på abacus -klosteret, der en kalkulerende stein med arabisk tall (cifra) var tilgjengelig for null, men ble brukt til andre formål i de abazistiske regneoperasjonene. Ved hjelp av den gamle og middelalderske abacus kunne addisjon og subtraksjon forenkles betraktelig, mens de ikke var veldig egnet for multiplikasjon og divisjon eller krevde relativt kompliserte operasjoner, som ble beskrevet spesielt for klosteret abacus i middelalderske traktater og var beryktet for deres vanskelighet.

Babylonierne utviklet først en tallfont med et fullverdig stedsverdisystem, der talltegnets posisjon også bestemmer verdien på grunnlag av 60, og sannsynligvis la til et eget tegn for null allerede på 400-tallet f.Kr. . ^[10] En tallfont med et stedsverdisystem på basen 10, men fremdeles uten tegn for null, ble sannsynligvis opprettet i Kina noen århundrer før århundreskiftet (bekreftet detaljer siden 2. århundre f.Kr.), sannsynligvis ved hjelp av en lysbildestyre Kinesisk variant av abacus delt inn i et rutemønster, og ble bare supplert med et symbol for null under indisk påvirkning fra 800 -tallet. ^[11]

I India selv kan begynnelsen på det posisjonelle desimalsystemet med tegn for null ikke bestemmes med sikkerhet. Det eldre Brahmi numeriske skriptet , som var i bruk fra 3. til 8. århundre, brukte et desimalsystem med tilnærminger til posisjonsskriving, men fortsatt uten et symbol for null. ^[12] Den eldste indiske formen for dagens indo-arabiske tall , med symboler for 1 til 9 og et punkt eller en liten sirkel for null, avledet fra Brahmi numerisk skrift, er først utenfor India siden 800-tallet takket være epigrafiske bevis som kan være pålitelig datert. i Sørøst -Asia som en indisk eksport og i India selv siden det 9. århundre; ^[13] men det antas at bruken av dette numeriske systemet begynte i India allerede på 500 -tallet. ^[14] Det samme posisjons desimalsystemet med tegn for null var også grunnlaget for det omtrent samtidige numeriske systemet med tall som ble undervist av indiske astronomer, der begrensende uttrykk som "begynnelse" (1), "øyne" (2), " de tre tidstrinnene "(3) for tallene 1 til 9 og" himmel "," tomhet "," punkt "eller andre ord for null ble rangert i henhold til deres desimal som en språklig beskrivelse av flersifrede tall. ^[15] Lokavibhaga , skrevet i Prakrit i 458 , regnes som tidlige bevis på en slik posisjonell setting av i dette tilfellet stort sett umetaforiske språklige numeriske betegnelser , ^[16] som imidlertid bare er bevart i en senere sanskrit -oversettelse . Det begrensende tallsystemet kan deretter bli funnet fullt utviklet i Bhaskara I (800 -tallet).

For skriving av tall vedtok araberne og menneskene som ble arabisert av dem i utgangspunktet desimaladditivsystemet for de alfabetiske greske tallene, først formidlet av de hebraiske og syriske modellene, og overført til de 28 bokstavene i det arabiske alfabetet. ^[17] Senest på 800-tallet ble imidlertid de indiske tallene og beregningsmetodene basert på dem først kjent i arabisk orient og i løpet av 900-tallet i Nord-Afrika og Al-Andalus . Den tidligste omtale ble funnet på 800 -tallet av den syriske biskopen Severus Sebokht , som uttrykkelig roser det indiske systemet. Muhammad ibn Musa al-Chwarizmi , som ikke bare brukte de nye sifrene i sine matematiske arbeider, men også en introduksjon, bare i latinsk oversettelse, Kitāb al-Jamʿ wa- l-tafrīq bi-ḥisāb al-Hind ("Om regning med indisk tall ") med en beskrivelse av det numeriske systemet som er egnet for nybegynnere og de grunnleggende skriftlige regneoperasjonene basert på dem.

I 10./11. På 1800 -tallet dukket det opp vestlige arabiske tall eller tall som stammer fra dem (kalt apices ) på kalkuleringssteinene i abacus -klosteret i Latin -vest. Imidlertid ble de ikke brukt utover det som tall eller til og med for skriftlig regning. Sammen med abacus -klosteret ble de glemt igjen. Al-Chwarizmi hjalp indiske tall med å få et gjennombrudd i latinske tilpasninger og relaterte folkespråklige avhandlinger siden 1100-tallet. Deres første ord Dixit Algorismi sørget for at "Algorism", den latinske gjengivelsen av navnet hans, etablerte seg bredt som navnet på denne nye regningskunsten. ^[18] Spesielt i Italia, hvor Leonardo Fibonacci gjorde det kjent i sin Liber abbaci fra sin egen kunnskap som ble oppnådd i Nord -Afrika , har den indiske numeriske beregningen vært i stand til å fullstendig erstatte abacus (med kalkstein) i finans og handel siden 1200 -tallet og til og med ta navnet (abbaco) . I andre land ble det gjenstand for vitenskapelig og kommersiell undervisning, men frem til tidlig moderne periode hadde den en overveldende konkurrent i regning på linjer. Selv som en enkel tallskrifttype for de praktiske formålene med å skrive ned tall og nummerere , som det ikke kreves noen systemverdisystem for, kunne de indo-arabiske tallene gradvis hevde seg mot de romerske tallene siden den tidlige moderne perioden.

Se også

Nummernavn

litteratur

John D. Barrow: Why the World is Mathematical / John D. Barrow. Fra engelskmennene og med et etterord av Herbert Mehrtens . Campus-Verl., Frankfurt / Main 1993, ISBN 3-593-34956-6 .
Georges Ifrah: Universell tallhistorie. Med fane. Og tegning. av forfatteren. Parkland-Verl., Köln 1998, ISBN 3-88059-956-4 .
Karl Menninger: nummer og nummer. Vol. 2. Numerisk skrift og regning . Vandenhoeck & Ruprecht, 1958.
John M. Pullan: Abacus 'historie . Hutchinson, London 1968.

weblenker

Wiktionary: Dezimalsystem – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Mathematik: Schulmathematik: Zahlensysteme: Zehnerzahlen – Lern- und Lehrmaterialien

Dezimal-/Zehnersystem für Schüler erklärt auf mathematik-wissen.de
Das dezimale Stellenwertsystem verstehen und metakognitiv denken lernen. Vorlagen mit flexiblen Interviews, es ist die Methode der kritischen Exploration, Piaget

Einzelnachweise

↑ Harald Haarmann: Weltgeschichte der Zahlen . Beck, München 2008, ISBN 978-3-406-56250-1 , S. 29 .
↑ Folge A051626 in OEIS
↑ Harald Krause, Sabrina Kutscher ua: Europas größter Spangenbarrenhort: Der frühbronzezeitliche Kupferschatz von Oberding. In: Matthias Wemhoff, Michael M. Rind: Bewegte Zeiten: Archäologie in Deutschland. Berlin, Petersberg 2018, S. 167 ff.
↑ J. Stolz: Erste Nachweise des Dezimalsystems? Der frühbronzezeitliche Spangenbarrenhort von Oberding. In: Restauro. Zeitschrift für Konservierung und Restaurierung , 8. Jahrgang 2017, S. 14–19.
↑ Menninger: Zahlwort und Ziffer (1958), II, S. 3ff.; Karl-August Wirth, Art. Fingerzahlen. In: Otto Schmidt (Hrsg.): Reallexikon zur deutschen Kunstgeschichte , Band VIII, Metzler Verlag, Stuttgart 1987, Sp. 1229–1310; Ifrah: Universalgeschichte der Zahlen (1998), S. 87.
↑ Menninger: Zahlwort und Ziffer (1958), II, S. 104ff.; Ifrah: Universalgeschichte der Zahlen (1998), S. 136ff.; Pullan, History of the Abacus (1968), S. 16ff.
↑ Menninger: Zahlwort und Ziffer (1958), S. 131ff; Ifrah: Universalgeschichte der Zahlen (1998), S. 530ff.; Werner Bergmann: Innovationen im Quadrivium des 10. und 11. Jahrhunderts. Studien zur Einführung von Astrolab und Abacus im lateinischen Mittelalter , Steiner Verlag, Stuttgart 1985 (= Sudhoffs Archiv, Beiheft 26), S. 57ff., S. 174ff.
↑ Alfred Nagl: Die Rechenpfennige und die operative Arithmetik. In: Numismatische Zeitschrift 19 (1887), S. 309–368; Menninger: Zahlwort und Ziffer (1958), II, S. 140ff.; Pullan: History of the Abacus (1968), passim
↑ Francis P. Barnard: The Casting-Counter and the Counting-Board. A Chapter in the History of Numismatics and Early Arithmetic , Clarendon Press, Oxford 1916; Menninger: Zahlwort und Ziffer (1958), II, S. 152ff., S. 165, S. 178, S. 182f.; Pullan: History of the Abacus (1968), S. 52ff.; Ifrah: Universalgeschichte der Zahlen (1998), S. 146ff.
↑ Ifrah: Universalgeschichte der Zahlen (1998), S. 411ff., S. 420.
↑ Ifrah: Universalgeschichte der Zahlen (1998), S. 428ff., S. 511ff.
↑ Ifrah. Universalgeschichte der Zahlen (1998), S. 504ff.
↑ Ifrah. Universalgeschichte der Zahlen (1998), S. 486ff.
↑ Ifrah: Universalgeschichte der Zahlen (1998), S. 498ff.
↑ Ifrah: Universalgeschichte der Zahlen (1998), S. 493ff.
↑ Ifrah: Universalgeschichte der Zahlen (1998), S. 499f.
↑ Ifrah: Universalgeschichte der Zahlen (1998), S. 307ff.
↑ Ifrah: Universalgeschichte der Zahlen (1998), S. 533ff.

[1] Harald Haarmann: Weltgeschichte der Zahlen . Beck, München 2008, ISBN 978-3-406-56250-1 , S. 29 .

[2] Folge A051626 in OEIS

[3] Harald Krause, Sabrina Kutscher ua: Europas größter Spangenbarrenhort: Der frühbronzezeitliche Kupferschatz von Oberding. In: Matthias Wemhoff, Michael M. Rind: Bewegte Zeiten: Archäologie in Deutschland. Berlin, Petersberg 2018, S. 167 ff.

[4] J. Stolz: Erste Nachweise des Dezimalsystems? Der frühbronzezeitliche Spangenbarrenhort von Oberding. In: Restauro. Zeitschrift für Konservierung und Restaurierung , 8. Jahrgang 2017, S. 14–19.

[5] Menninger: Zahlwort und Ziffer (1958), II, S. 3ff.; Karl-August Wirth, Art. Fingerzahlen. In: Otto Schmidt (Hrsg.): Reallexikon zur deutschen Kunstgeschichte , Band VIII, Metzler Verlag, Stuttgart 1987, Sp. 1229–1310; Ifrah: Universalgeschichte der Zahlen (1998), S. 87.

[6] Menninger: Zahlwort und Ziffer (1958), II, S. 104ff.; Ifrah: Universalgeschichte der Zahlen (1998), S. 136ff.; Pullan, History of the Abacus (1968), S. 16ff.

[7] Menninger: Zahlwort und Ziffer (1958), S. 131ff; Ifrah: Universalgeschichte der Zahlen (1998), S. 530ff.; Werner Bergmann: Innovationen im Quadrivium des 10. und 11. Jahrhunderts. Studien zur Einführung von Astrolab und Abacus im lateinischen Mittelalter , Steiner Verlag, Stuttgart 1985 (= Sudhoffs Archiv, Beiheft 26), S. 57ff., S. 174ff.

[8] Alfred Nagl: Die Rechenpfennige und die operative Arithmetik. In: Numismatische Zeitschrift 19 (1887), S. 309–368; Menninger: Zahlwort und Ziffer (1958), II, S. 140ff.; Pullan: History of the Abacus (1968), passim

[9] Francis P. Barnard: The Casting-Counter and the Counting-Board. A Chapter in the History of Numismatics and Early Arithmetic , Clarendon Press, Oxford 1916; Menninger: Zahlwort und Ziffer (1958), II, S. 152ff., S. 165, S. 178, S. 182f.; Pullan: History of the Abacus (1968), S. 52ff.; Ifrah: Universalgeschichte der Zahlen (1998), S. 146ff.

[10] Ifrah: Universalgeschichte der Zahlen (1998), S. 411ff., S. 420.

[11] Ifrah: Universalgeschichte der Zahlen (1998), S. 428ff., S. 511ff.

[12] Ifrah. Universalgeschichte der Zahlen (1998), S. 504ff.

[13] Ifrah. Universalgeschichte der Zahlen (1998), S. 486ff.

[14] Ifrah: Universalgeschichte der Zahlen (1998), S. 498ff.

[15] Ifrah: Universalgeschichte der Zahlen (1998), S. 493ff.

[16] Ifrah: Universalgeschichte der Zahlen (1998), S. 499f.

[17] Ifrah: Universalgeschichte der Zahlen (1998), S. 307ff.

[18] Ifrah: Universalgeschichte der Zahlen (1998), S. 533ff.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]